Question

（2012•天津）已知函数y=

|x2-1|

x-1

的图象与函数y=kx的图象恰有两个交点，则实数k的取值范围是

（0，1）∪（1，2）

．

Answer 1

分析：函数y=

|x2-1|

x-1

=

|x+1| • |x-1|

x-1

=

x+1  ， x＞1 -(x+1) ，  -1≤ x＜1 x+1 ，   x＜-1

，如图所示，可得直线y=kx与函数y=

|x2-1|

x-1

的图象相交于两点时，直线的斜率k的取值范围．

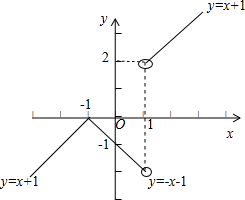解答：解：函数y=

|x2-1|

x-1

=

|x+1| • |x-1|

x-1

=

x+1  ， x＞1 -(x+1) ，  -1≤ x＜1 x+1 ，   x＜-1

，
如图所示：
故当一次函数y=kx的斜率k满足0＜k＜1 或1＜k＜2时，
直线y=kx与函数y=

|x2-1|

x-1

的图象相交于两点，
故答案为 （0，1）∪（1，2）．

点评：本题主要考查函数的零点的定义，函数的零点与方程的根的关系，体现了转化、数形结合的数学思想，
属于基础题．