题目内容
在正项等比数列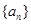 中,
中,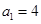 ,
, 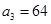 .
.
(1) 求数列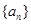 的通项公式
的通项公式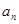 ;
;
(2) 记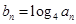 ,求数列
,求数列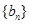 的前n项和
的前n项和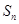 ;
;
(3) 记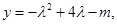 对于(2)中的
对于(2)中的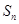 ,不等式
,不等式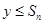 对一切正整数n及任意实数
对一切正整数n及任意实数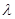 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
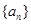 中,
中,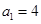 ,
, 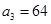 .
.(1) 求数列
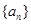 的通项公式
的通项公式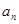 ;
; (2) 记
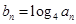 ,求数列
,求数列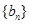 的前n项和
的前n项和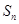 ;
;(3) 记
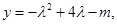 对于(2)中的
对于(2)中的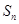 ,不等式
,不等式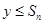 对一切正整数n及任意实数
对一切正整数n及任意实数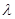 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.(1)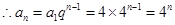
(2)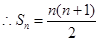
(3)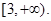
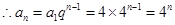
(2)
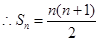
(3)
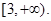
试题分析:解:(1).
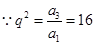 ,解得
,解得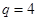 或
或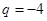 (舍去)
(舍去) 
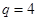 2分
2分 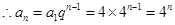 3分 (
3分 (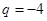 没有舍去的得2分)
没有舍去的得2分)(2)
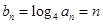 , 5分
, 5分 数列
数列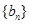 是首项
是首项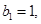 公差
公差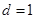 的等差数列
的等差数列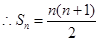 7分
7分(3)解法1:由(2)知,
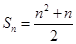 ,
,当n=1时,
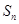 取得最小值
取得最小值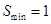 8分
8分要使对一切正整数n及任意实数
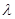 有
有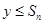 恒成立,
恒成立,即
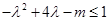
即对任意实数
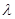 ,
, 恒成立,
恒成立,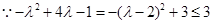 ,
, 所以
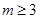 ,
,故
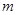 得取值范围是
得取值范围是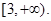 10分
10分解法2:由题意得:
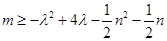 对一切正整数n及任意实数
对一切正整数n及任意实数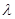 恒成立,
恒成立,即
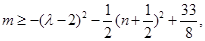
因为
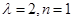 时,
时,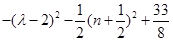 有最小值3,
有最小值3,所以
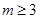 ,
,故
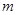 得取值范围是
得取值范围是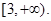 10分
10分点评:主要是以等比数列为背景来求解通项公式和求和,以及不等式的恒成立问题来求解参数的范围,属于中档题。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
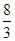 和
和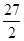 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为 .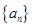 中,
中,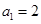 ,
,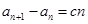 (
(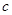 是常数,
是常数,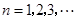 ),且
),且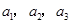 成公比不为
成公比不为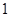 的等比数列.
的等比数列.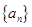 的前n项和为
的前n项和为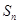 ,若
,若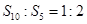 ,则
,则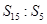 的值为
的值为 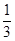
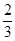
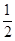
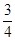
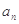 }的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.
}的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.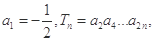 ,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由。
,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由。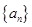 中,若
中,若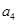 ,
,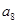 是方程
是方程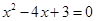 的两根,则
的两根,则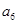 的值是( )
的值是( )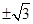
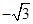
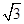

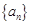 的各项都为正数,它的前三项依次为1,
的各项都为正数,它的前三项依次为1,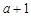 ,
,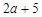 ,则数列
,则数列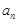 ="_____________"
="_____________"  为递增数列,且
为递增数列,且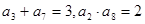 ,则
,则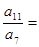 ________.
________.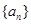 是首项为
是首项为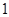 ,公比为
,公比为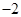 的等比数列,则
的等比数列,则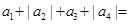 .
.