题目内容
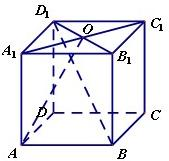 棱长为2的正方体ABCD-A1B1C1D1中,A1C1∩B1D1=O.
棱长为2的正方体ABCD-A1B1C1D1中,A1C1∩B1D1=O.①求异面直线OA与BD1所成角的余弦值;
②求OA与平面BB1D1D所成角的余弦值.
分析:①取BB1中点M,连接MA,M0,可证得∠AOM即异面直线OA与BD1所成角在三角形AOM中求解即可;
②连接BD,AC交于一点N,连接ON,可证得∠AON即所求的OA与平面BB1D1D所成角,在直角三角形ANO中求其余弦值即可.
②连接BD,AC交于一点N,连接ON,可证得∠AON即所求的OA与平面BB1D1D所成角,在直角三角形ANO中求其余弦值即可.
解答: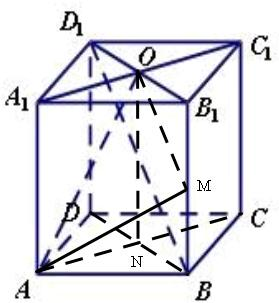 解:①如图取BB1中点M,连接MA,M0,由正方体的性质知,OM∥BD1,故∠AOM即异面直线OA与BD1所成角
解:①如图取BB1中点M,连接MA,M0,由正方体的性质知,OM∥BD1,故∠AOM即异面直线OA与BD1所成角
由于正方体的棱长为2,故B1M=1,B1O=
由勾股定理求得OM=
,
同理可求得AO=
,AM=
在△AMO中,由余弦定理知cos∠AOM=
=
;
②如图连接BD,AC交于一点N,连接ON,N是底面的中心,连接ON,知ON=2,由正方体的性质知AN垂直面BB1D1D,故∠AON即所求的OA与平面BB1D1D所成角,
在直角三角形AA1O中,cos∠AON=
=
即OA与平面BB1D1D所成角的余弦值是
 解:①如图取BB1中点M,连接MA,M0,由正方体的性质知,OM∥BD1,故∠AOM即异面直线OA与BD1所成角
解:①如图取BB1中点M,连接MA,M0,由正方体的性质知,OM∥BD1,故∠AOM即异面直线OA与BD1所成角由于正方体的棱长为2,故B1M=1,B1O=
| 2 |
| 3 |
同理可求得AO=
| 6 |
| 5 |
在△AMO中,由余弦定理知cos∠AOM=
| 3+6-5 | ||||
2×
|
| ||
| 3 |
②如图连接BD,AC交于一点N,连接ON,N是底面的中心,连接ON,知ON=2,由正方体的性质知AN垂直面BB1D1D,故∠AON即所求的OA与平面BB1D1D所成角,
在直角三角形AA1O中,cos∠AON=
| 2 | ||
|
| ||
| 3 |
即OA与平面BB1D1D所成角的余弦值是
| ||
| 3 |
点评:本题考查了求异面直线的方法与求线面角的方法,此两类角的求法都要注意做题步骤,做角,证角,求角,勿因忘记证明失分,此是本类题的易错点,切记!

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
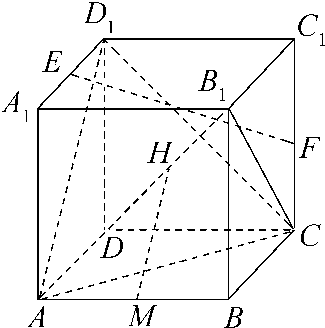 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.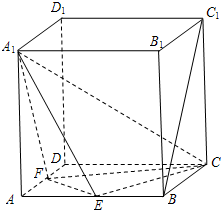 (2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
(2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求: