题目内容
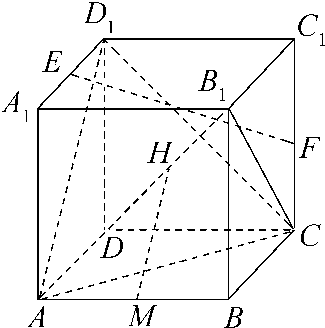 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.(1)求证:EF∥平面ACD1;
(2)求证:MH⊥B1C;
(3)在棱BB1上是否存在一点P,使得二面角P-AC-B的大小为30°?若存在,求出BP的长;若不存在,请说明理由.
分析:(1)由于ABCD-A1B1C1D1为正方体且边长为2,并且E、F、M、H分别为A1D1、CC1、AB、DB1的中点,利用正方体的性质及要证明的问题可以取AA1的中点G,连接GF,则GF∥AC,在利用线面平行的判定定理即可得证;
(2)由题意可以连接AC1,,由于H为可以得到为AC1的中点,连接BC1,设BC1交B1C于点O,在正方形中利用正方形的性质即可得到BC1⊥B1C,而MH∥BC1所以可以得到MH⊥B1C;
(3)由题意可以建立分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,写出各点的坐标,进而求出所要求解的平面的法向量,利用平面的法向量的夹角与二面角的大小之间的关系即可求出二面角P-AC-B的大小.
(2)由题意可以连接AC1,,由于H为可以得到为AC1的中点,连接BC1,设BC1交B1C于点O,在正方形中利用正方形的性质即可得到BC1⊥B1C,而MH∥BC1所以可以得到MH⊥B1C;
(3)由题意可以建立分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,写出各点的坐标,进而求出所要求解的平面的法向量,利用平面的法向量的夹角与二面角的大小之间的关系即可求出二面角P-AC-B的大小.
解答: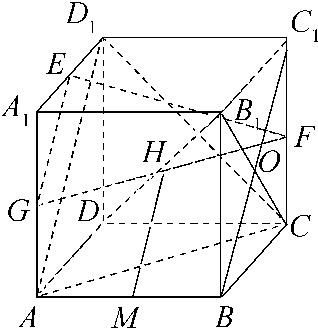 解:(1)取AA1的中点G,连接GF,则GF∥AC,
解:(1)取AA1的中点G,连接GF,则GF∥AC,
连接GE取AA1的中点G,连接GF,则GF∥AC,
则GE∥AD1,
∴平面ACD1∥平面GFE.
又∵EF?平面GFE,
∴EF∥平面ACD1.
(2)连接AC1,
∵H为DB1的中点,
∴H为AC1的中点,连接BC1,设BC1交B1C于点O,
∵M为AB的中点,
∴MH∥BC1.
在正方形BCC1B1中,BC1⊥B1C,
∴MH⊥B1C.
(3)如图,分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,
则由已知得D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),B1(2,2,2).
设点P(2,2,t)(0<t≤2),
平面ACP的一个法向量为n=(x,y,z),则
.
∵
=(-2,2,0),
=(0,2,t),
∴
,取n=(1,1,-
).
易知平面ABC的一个法向量为
=(0,0,2),
假设P点存在,使得二面角P-AC-B的大小为θ=30°,
则cosθ=|cos<
,n>|=
=
,
即
=
(2+
),解得t=
.
∴
∈(0,2],∴在棱BB1上存在一点P,当BP的长为
时,二面角P-AC-B的大小为30°.
 解:(1)取AA1的中点G,连接GF,则GF∥AC,
解:(1)取AA1的中点G,连接GF,则GF∥AC,连接GE取AA1的中点G,连接GF,则GF∥AC,
则GE∥AD1,
∴平面ACD1∥平面GFE.
又∵EF?平面GFE,
∴EF∥平面ACD1.
(2)连接AC1,
∵H为DB1的中点,
∴H为AC1的中点,连接BC1,设BC1交B1C于点O,
∵M为AB的中点,
∴MH∥BC1.
在正方形BCC1B1中,BC1⊥B1C,
∴MH⊥B1C.
(3)如图,分别以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,
则由已知得D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),B1(2,2,2).
设点P(2,2,t)(0<t≤2),
平面ACP的一个法向量为n=(x,y,z),则
|
∵
| AC |
| AP |
∴
|
| 2 |
| t |
易知平面ABC的一个法向量为
| B1B |
假设P点存在,使得二面角P-AC-B的大小为θ=30°,
则cosθ=|cos<
| BB1 |
|-
| ||||
2×
|
| ||
| 2 |
即
| 4 |
| t2 |
| 3 |
| 4 |
| 4 |
| t2 |
| ||
| 3 |
∴
| ||
| 3 |
| ||
| 3 |
点评:(1)此问考查了正方形及正方体的基本性质,还考查了线面平行的判定定理,及学生的空间想象能力;
(2)此问考查了正方形的性质及两条直线所成角的概念;
(3)此问考查了利用空间想象能力及利用二面角的大小与平面的法向量的夹角之间的关系求解二面角的方法.
(2)此问考查了正方形的性质及两条直线所成角的概念;
(3)此问考查了利用空间想象能力及利用二面角的大小与平面的法向量的夹角之间的关系求解二面角的方法.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )






