Question

在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E，F分别为棱AB和CC₁的中点，则线段EF被正方体的内切球球面截在球内的线段长为

 

．

Answer 1

分析：先画出图形，确定过EF和球心的截面的位置，利用三角形相似关系，求出球心到EF的距离，然后解出线段EF被正方体的内切球球面截在球内的线段长．

解答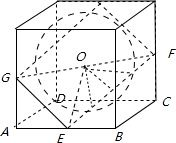：解：由题意画出图形：
则过EF和球心的截面，G为侧棱棱AA₁的中点，
易证EF⊥GE，GE=

2

，
则O到线段EF的距离为

2

2

，又球的半径为1，
所以：线段EF被正方体的内切球球面截在球内的线段长为
2×

2

2

=

2

故答案为：

2

点评：本题考查正方体的内接球问题，考查空间想象能力，逻辑思维能力，是中档题．