题目内容
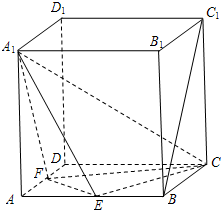 (2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
(2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:(1)异面直线BC1与EF所成角的大小;
(2)三棱锥A1-EFC的体积V.
分析:(1)因为点E、F分别是棱AB、AD的中点,所以EF∥BD⇒∠C1BD是异面直线BC1与EF所成的角;在△DBC1中,求出∠C1BD即可;
(2)先求出三角形EFC的面积,再根据A1A即为三棱锥的高代入体积计算公式即可.
(2)先求出三角形EFC的面积,再根据A1A即为三棱锥的高代入体积计算公式即可.
解答:解:(1)因为点E、F分别是棱AB、AD的中点,所以EF∥BD,
所以∠C1BD是异面直线BC1与EF所成的角. (4分)
在△DBC1中,∠C1BD=60°.
所以异面直线BC1与EF所成角的大小为60°. (8分)
(2)因为:S△EFC=SABCD-S△AEF-S△CDF-S△BCE=2×2-
×1×1-
×2×1-
×2×1=
.
∴VA1-EFC=
AA1•S△EFC=
×2×
=1.(14分)
所以∠C1BD是异面直线BC1与EF所成的角. (4分)
在△DBC1中,∠C1BD=60°.
所以异面直线BC1与EF所成角的大小为60°. (8分)
(2)因为:S△EFC=SABCD-S△AEF-S△CDF-S△BCE=2×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴VA1-EFC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
点评:本题主要考查异面直线及其所成的角以及三棱锥的体积计算.解决第二问的关键在于对公式的熟练掌握.

练习册系列答案
相关题目