题目内容
已知向量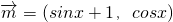 ,
,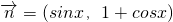 ,设函数
,设函数 ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期;
(2)若x∈[0,π],求函数f(x)值域.
解:(1)由题意可得,函数f(x)= =sinx(sinx+1)+cosx(cosx+1)=1+sinx+cosx=1+
=sinx(sinx+1)+cosx(cosx+1)=1+sinx+cosx=1+ sin(x+
sin(x+ ),故函数的周期等于
),故函数的周期等于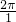 =2 π.
=2 π.
(2)若x∈[0,π],则 ≤x+
≤x+ ≤
≤ ,∴-
,∴- ≤sin(x+
≤sin(x+ )≤1,∴1-
)≤1,∴1- ×
× ≤f(x)≤1+
≤f(x)≤1+ ,故函数f(x)的值域为[0,1+
,故函数f(x)的值域为[0,1+ ].
].
分析:(1)利用两角和差的正弦公式化简函数f(x)的解析式为1+ sin(x+
sin(x+ ),由此可得函数的最小正周期.
),由此可得函数的最小正周期.
(2)若x∈[0,π],则 ≤x+
≤x+ ≤
≤ ,由此求得sin(x+
,由此求得sin(x+ ) 的值域,即可求得函数f(x)值域.
) 的值域,即可求得函数f(x)值域.
点评:本题主要考查两个向量的数量积公式,本题主要考查两角和差的正弦公式、二倍角公式的应用,正弦函数的定义域和值域,属于中档题.
 =sinx(sinx+1)+cosx(cosx+1)=1+sinx+cosx=1+
=sinx(sinx+1)+cosx(cosx+1)=1+sinx+cosx=1+ sin(x+
sin(x+ ),故函数的周期等于
),故函数的周期等于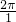 =2 π.
=2 π.(2)若x∈[0,π],则
 ≤x+
≤x+ ≤
≤ ,∴-
,∴- ≤sin(x+
≤sin(x+ )≤1,∴1-
)≤1,∴1- ×
× ≤f(x)≤1+
≤f(x)≤1+ ,故函数f(x)的值域为[0,1+
,故函数f(x)的值域为[0,1+ ].
].分析:(1)利用两角和差的正弦公式化简函数f(x)的解析式为1+
 sin(x+
sin(x+ ),由此可得函数的最小正周期.
),由此可得函数的最小正周期.(2)若x∈[0,π],则
 ≤x+
≤x+ ≤
≤ ,由此求得sin(x+
,由此求得sin(x+ ) 的值域,即可求得函数f(x)值域.
) 的值域,即可求得函数f(x)值域.点评:本题主要考查两个向量的数量积公式,本题主要考查两角和差的正弦公式、二倍角公式的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,设函数
,设函数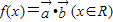 的图象关于直线
的图象关于直线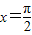 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围. ,
, ,设函数
,设函数 •
• ,若函数g(x)的图象与f(x)的图象关于坐标原点对称.
,若函数g(x)的图象与f(x)的图象关于坐标原点对称. ]上的最大值,并求出此时x的值;
]上的最大值,并求出此时x的值; ,b+c=7,△ABC的面积为2
,b+c=7,△ABC的面积为2 ,求边a的长.
,求边a的长. ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
, ,设函数
,设函数 .
. 的最小正周期;
的最小正周期; 中,若
中,若 的面积为
的面积为 ,求实数
,求实数 的值.
的值.