题目内容
已知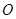 为平面上的定点,
为平面上的定点,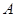 、
、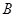 、
、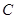 是平面上不共线的三点,若
是平面上不共线的三点,若
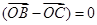 ,则DABC是( )
,则DABC是( )
| A.以AB为底边的等腰三角形 | B.以BC为底边的等腰三角形 |
| C.以AB为斜边的直角三角形 | D.以BC为斜边的直角三角形 |
B
解析试题分析:根据题意,涉及了向量的加减法运算,以及数量积运算。
因此可知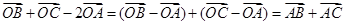
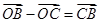 ,所以
,所以
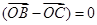 可知为
可知为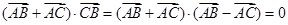
故有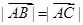 ,因此可知b=c,说明了是一个以BC为底边的等腰三角形,故选B.
,因此可知b=c,说明了是一个以BC为底边的等腰三角形,故选B.
考点:本试题主要考查了向量的数量积的运用。
点评:解决该试题的关键是利用向量的加减法灵活的变形,得到长度b=c,然后分析得到形状,注意多个变量,向一组基向量的变形技巧。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
 是边长为
是边长为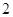 的正三角形,则
的正三角形,则 =( )
=( )
A. | B. | C.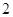 | D. |
在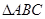 中,
中,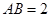 ,
,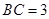 ,
,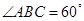 ,
,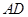 为
为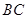 边上的高,
边上的高, 为
为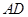 的中点,若
的中点,若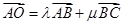 ,则
,则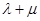 的值为()
的值为()
A.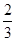 | B.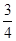 | C.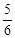 | D.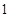 |
已知向量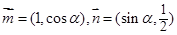 ,且
,且 ,则
,则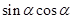 等于
等于
A. | B.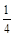 | C. | D. |
设 =(2
=(2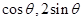 ),
),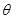
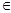 (
(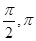 );
); =(0,-1),则
=(0,-1),则 与
与 夹角为
夹角为
A.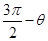 | B.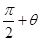 | C.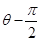 | D.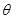 |
设 是不共线的两个向量,已知
是不共线的两个向量,已知 ,
, ,
, .若
.若
三点共线,则 的值为 ( )
的值为 ( )
| A.1 | B.2 | C.-2 | D.-1 |
设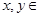 R,向量
R,向量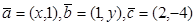 且
且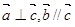 ,则
,则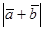 ( )
( )
A.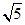 | B. | C.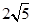 | D.10 |
对于直角坐标平面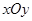 内的点
内的点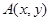 (不是原点),
(不是原点),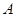 的“对偶点”
的“对偶点”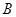 是指:满足
是指:满足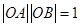 且在射线
且在射线 上的那个点. 若
上的那个点. 若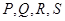 是在同一直线上的四个不同的点(都不是原点),则它们的“对偶点”
是在同一直线上的四个不同的点(都不是原点),则它们的“对偶点”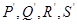 ( )
( )
| A.一定共线 | B.一定共圆 |
| C.要么共线,要么共圆 | D.既不共线,也不共圆 |
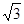 sinA,sinB),n=(cosB,
sinA,sinB),n=(cosB, B.
B. 
 D.
D. 