题目内容
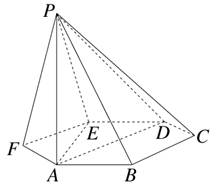
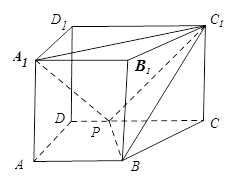
在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF的中点,BN⊥CE.
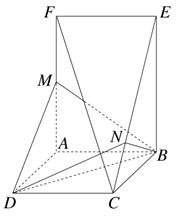
(1)求证:CF∥平面MBD;
(2)求证:CF⊥平面BDN.

(1)求证:CF∥平面MBD;
(2)求证:CF⊥平面BDN.
(1)见解析 (2)见解析
证明:(1)连接AC交BD于点O,连接OM.
因为四边形ABCD是正方形,所以O为AC的中点.
因为M为AF的中点,所以CF∥OM,
又OM?平面MBD,CF?平面MBD,所以CF∥平面MBD.
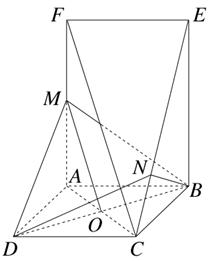
(2)因为正方形ABCD和矩形ABEF所在的平面互相垂直,
所以AF⊥平面ABCD,又BD?平面ABCD,所以AF⊥BD.
又四边形ABCD是正方形,所以AC⊥BD.
因为AC∩AF=A,所以BD⊥平面ACF,
因为CF?平面ACF,所以CF⊥BD.
因为AB⊥BC,AB⊥BE,BC∩BE=B,所以AB⊥平面BCE.
因为BN?平面BCE,所以AB⊥BN,易知EF∥AB,
所以EF⊥BN.
又EC⊥BN,EF∩EC=E,所以BN⊥平面CEF,
因为CF?平面CEF,所以BN⊥CF.
因为BD∩BN=B,所以CF⊥平面BDN.
因为四边形ABCD是正方形,所以O为AC的中点.
因为M为AF的中点,所以CF∥OM,
又OM?平面MBD,CF?平面MBD,所以CF∥平面MBD.

(2)因为正方形ABCD和矩形ABEF所在的平面互相垂直,
所以AF⊥平面ABCD,又BD?平面ABCD,所以AF⊥BD.
又四边形ABCD是正方形,所以AC⊥BD.
因为AC∩AF=A,所以BD⊥平面ACF,
因为CF?平面ACF,所以CF⊥BD.
因为AB⊥BC,AB⊥BE,BC∩BE=B,所以AB⊥平面BCE.
因为BN?平面BCE,所以AB⊥BN,易知EF∥AB,
所以EF⊥BN.
又EC⊥BN,EF∩EC=E,所以BN⊥平面CEF,
因为CF?平面CEF,所以BN⊥CF.
因为BD∩BN=B,所以CF⊥平面BDN.

练习册系列答案
相关题目
 中,
中,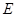 是
是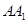 的中点.
的中点.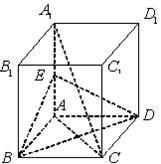
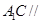 平面
平面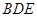 ;
;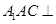 平面
平面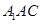 所成角的正弦值.
所成角的正弦值.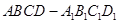 底面
底面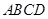 直角梯形,
直角梯形,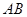 ∥
∥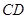 ,
,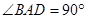 ,
,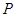 是棱
是棱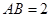 ,
,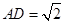 ,
,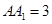 ,
,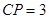 ,
,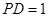 .
.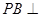 平面
平面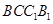 .
.
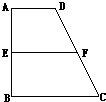 已知梯形ABCD中,AD
已知梯形ABCD中,AD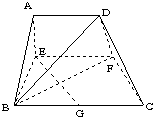
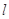 ,
,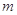 ,
,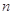 为三条不同的直线,
为三条不同的直线,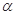 ,
,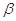 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( ) 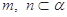 ,则
,则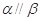 .
.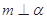 ,
,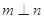 ,则
,则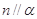 .
.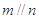 ,
,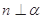 ,则
,则