题目内容
18.等差数列{an}的前n项和为Sn,若a1+a9+a11=30,则S13=130.分析 由题意和等差数列的性质可得a7,再由等差数列的性质和求和公式可得S13=13a7,代值计算可得.
解答 解:由等差数列的性质可得a1+a9+a11=a1+a11+a9
=a5+a7+a9=3a7=30,解得a7=10,
∴S13=$\frac{13({a}_{1}+{a}_{13})}{2}$=$\frac{13×2{a}_{7}}{2}$=13a7=130,
故答案为:130.
点评 本题考查等差数列的求和公式和性质,求出数列a7是解决问题的关键,属基础题.

练习册系列答案
相关题目
13.已知函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,则f($\frac{1}{11}$)+f($\frac{2}{11}$)+…+f($\frac{10}{11}$)的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
3.函数f(x)=$\sqrt{{x}^{2}-x-2}$的单调递增区间为( )
| A. | [2,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,+∞) | D. | (-∞,-1] |
10.下列分别为集合A到集合B的对应:其中,是从A到B的映射的是( )
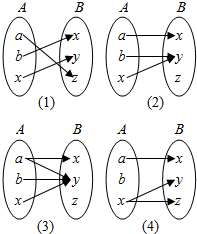

| A. | (1)(2) | B. | (1)(2)( 3) | C. | (1)(2)(4) | D. | (1)(2)(3)(4) |
8.下列命题中的假命题是( )
| A. | ?x∈R,ex>0 | B. | ?x∈R,lnx=0 | C. | ?x∈R,(x-1)2≥0 | D. | ?x∈R,x2+1=0 |