题目内容
已知函数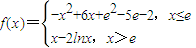
（其中e为自然对数的底数，且e≈2.718）若f（6-a2）＞f（a），则实数a的取值范围是 ．
【答案】分析：利用二次函数的单调性，及导数工具，先探讨函数的单调性，然后利用条件列出不等式，即可解得a的范围．
解答：解：∵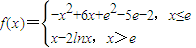
∴当x≤e时y=-（x-3）2+e2-5e+7∴x≤e时函数单调递增 当x＞e时y'=1-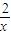
＞0恒成立，故x＞e时函数单调递增，
∵f（e）=e-2=e-2lne∴函数在R上为增函数．
∴由f（6-a2）＞f（a）得6-a2＞a，
解得-3＜a＜2
故答案为-3＜a＜2
点评：本题考查了函数单调性的性质及利用导数研究函数的单调性，在探讨分段函数的性质时注意分段研究．本题是个中档题．
解答：解：∵
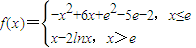
∴当x≤e时y=-（x-3）2+e2-5e+7∴x≤e时函数单调递增 当x＞e时y'=1-
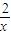＞0恒成立，故x＞e时函数单调递增，∵f（e）=e-2=e-2lne∴函数在R上为增函数．
∴由f（6-a2）＞f（a）得6-a2＞a，
解得-3＜a＜2
故答案为-3＜a＜2
点评：本题考查了函数单调性的性质及利用导数研究函数的单调性，在探讨分段函数的性质时注意分段研究．本题是个中档题．
练习册系列答案
相关题目
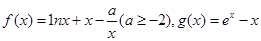（其中e为自然对数）
的极值。
（常数a>0），当x>1时，求函数G(x)的单调区
，其中e为自然对数的底数，且当x>0时
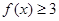恒成立．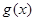
的单调区间；
.
（其中e为自然对数）
的极值。
（常数a>0），当x>1时，求函数G(x)的单调区间，并在极值存在处求极值。
，其中e为自然对数的底数．
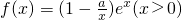，其中e为自然对数的底数．
在（1，l：x=1）处的切线与坐标轴围成的面积；
存在一个极大值点和一个极小值点，且极大值与极小值的积为e5，求a的值．