题目内容
（1）利用定义证明：函数f（x）=x3-3x在[0，1]上单调递减，在[1，+∞）上单调递增；
（2）设x0是方程x3-3x=100的正实数解，利用（1）的结论，求证：4＜x0＜5．
（2）设x0是方程x3-3x=100的正实数解，利用（1）的结论，求证：4＜x0＜5．
分析：（1）根据函数单调性的证明步骤：取值-作差-变形-判断符号-下结论，在对应的定义域内进行取值，判断符号时需要分类讨论；
（2）先对函数解析式进行化简，判断出x0所在的单调区间，再由单调性和f（4）=52、f（5）=110，证明出结论正确．
（2）先对函数解析式进行化简，判断出x0所在的单调区间，再由单调性和f（4）=52、f（5）=110，证明出结论正确．
解答：解：（1）任取x1，x2∈[0，+∞），且x1＜x2
∴f（x1）-f（x2）=（x13-3x1）-（x23-3x2）
∵0≤x1＜x2，即x1-x2＜0
当x1，x2∈[0，1]时，x12+x1x2+x22-3＜0，有f（x1）-f（x2）＞0，
即f（x1）＞f（x2）；
当x1，x2∈[1，+∞）时，x12+x1x2+x22-3＞0，有f（x1）-f（x2）＜0，
即f（x1）＜f（x2）；
由单调性定义得：f（x）=x3-3x在[0，1]上单调减，在[1，+∞）上单调增；
（2）由于f（x）=x3-3x=x（x2-3），当0≤x≤
时，f（x）≤0＜100，
∴方程x3-3x=100的正实数解x0＞
又∵f（x）=x3-3x在[1，+∞）上的增函数，且f（x0）=100，f（4）=52，f（5）=110，
∴f（4）＜f（x0）＜f（5），即4＜x0＜5．
∴f（x1）-f（x2）=（x13-3x1）-（x23-3x2）
|
∵0≤x1＜x2，即x1-x2＜0
当x1，x2∈[0，1]时，x12+x1x2+x22-3＜0，有f（x1）-f（x2）＞0，
即f（x1）＞f（x2）；
当x1，x2∈[1，+∞）时，x12+x1x2+x22-3＞0，有f（x1）-f（x2）＜0，
即f（x1）＜f（x2）；
由单调性定义得：f（x）=x3-3x在[0，1]上单调减，在[1，+∞）上单调增；
（2）由于f（x）=x3-3x=x（x2-3），当0≤x≤
| 3 |
∴方程x3-3x=100的正实数解x0＞
| 3 |
又∵f（x）=x3-3x在[1，+∞）上的增函数，且f（x0）=100，f（4）=52，f（5）=110，
∴f（4）＜f（x0）＜f（5），即4＜x0＜5．
点评：本题考查了函数单调性的证明以及应用，利用定义法证明函数的单调性时，必须遵循取值-作差-变形-判断符号-下结论这个步骤，涉及了分类讨论思想．
练习册系列答案
习题精选系列答案
相关题目
在
上是增函数，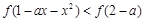
对于任意
恒成立，求实数
的取值范围。