题目内容
1.已知向量$\overline{a}$=(x-1,2),$\overline{b}$=(2,1),则“x>0”是“$\overline{a}$与$\overline{b}$夹角为锐角”的( )| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义以及向量的数量积的应用,进行判断即可.
解答 解:若$\overline{a}$与$\overline{b}$夹角为锐角,则$\overline{a}$•$\overline{b}$=(x-1,2)•(2,1)=2x>0,解得x>0成立,
若$\overline{a}$与$\overline{b}$同向共线时,满足$\frac{x-1}{2}=\frac{2}{1}$,解得x=5,满足x>0,但此时夹角为0°,不是锐角,
故“x>0”是“$\overline{a}$与$\overline{b}$夹角为锐角”的必要不充分条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,根据向量的数量积的应用是解决本题的关键.

练习册系列答案
相关题目
11.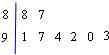 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
叶为个位数,则这组数据的中位数和平均数分别是( )
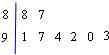 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是( )
| A. | 91,91.5 | B. | 91,92 | C. | 91.5,91.5 | D. | 91.5,92 |
16.集合M={x|lgx>0},N={x|x2≤4},则M∩N=( )
| A. | (0,2] | B. | (0,2) | C. | (1,2] | D. | (1,2) |
6.圆(x-a)2+y2=1与直线y=x相切于第三象限,则a=( )
| A. | -2 | B. | 2 | C. | $-\sqrt{2}$ | D. | $\sqrt{2}$ |
10.一个四棱锥的三视图如图所示,其侧视图是等边三角形.则该四棱锥的体积等于( )


| A. | $8\sqrt{3}$ | B. | $16\sqrt{3}$ | C. | $24\sqrt{3}$ | D. | $48\sqrt{3}$ |
 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.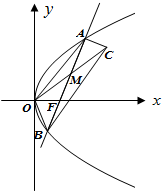 已知抛物线的顶点在原点,焦点F在x轴上,且抛物线上横坐标为1的点到F的距离为2,过点F的直线交抛物线于A,B两点.
已知抛物线的顶点在原点,焦点F在x轴上,且抛物线上横坐标为1的点到F的距离为2,过点F的直线交抛物线于A,B两点.