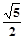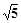题目内容
已知椭圆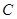 :
: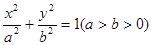 ,左、右两个焦点分别为
,左、右两个焦点分别为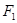 、
、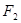 ,上顶点
,上顶点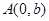 ,
,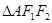 为正三角形且周长为6.
为正三角形且周长为6.
(1)求椭圆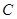 的标准方程及离心率;
的标准方程及离心率;
(2)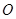 为坐标原点,
为坐标原点,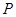 是直线
是直线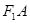 上的一个动点,求
上的一个动点,求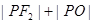 的最小值,并求出此时点
的最小值,并求出此时点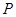 的坐标.
的坐标.
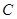 :
: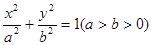 ,左、右两个焦点分别为
,左、右两个焦点分别为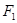 、
、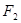 ,上顶点
,上顶点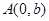 ,
,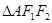 为正三角形且周长为6.
为正三角形且周长为6.(1)求椭圆
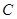 的标准方程及离心率;
的标准方程及离心率;(2)
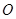 为坐标原点,
为坐标原点,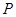 是直线
是直线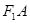 上的一个动点,求
上的一个动点,求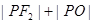 的最小值,并求出此时点
的最小值,并求出此时点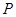 的坐标.
的坐标.(1)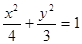 , 离心率
, 离心率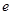
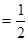 (2)
(2)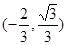
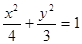 , 离心率
, 离心率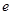
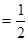 (2)
(2)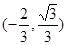
试题分析:解:(Ⅰ)解:由题设得
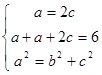 2分
2分解得:
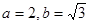 ,
,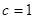 …… 3分
…… 3分故
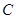 的方程为
的方程为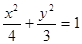 . …… 5分 离心率
. …… 5分 离心率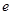
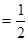 6分
6分(2)直线
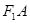 的方程为
的方程为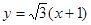 , 7分
, 7分设点
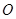 关于直线
关于直线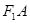 对称的点为
对称的点为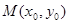 ,则
,则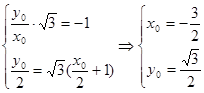 (联立方程正确,可得分至8分)
(联立方程正确,可得分至8分)所以点
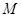 的坐标为
的坐标为 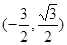 9分
9分∵
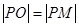 ,
,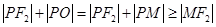 ,…… 10分
,…… 10分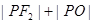 的最小值为
的最小值为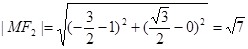 11分
11分直线
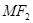 的方程为
的方程为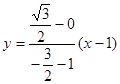 即
即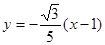 12分
12分由
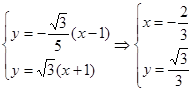 ,所以此时点
,所以此时点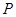 的坐标为
的坐标为 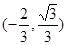 14分
14分点评:解决的关键是通过其简单几何性质以及直线于椭圆方程的联立方程组来求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 到点
到点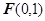 的距离与点
的距离与点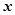 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点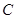 的方程;(II)过点
的方程;(II)过点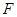 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线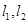 ,设
,设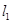 与轨迹
与轨迹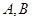 ,
,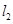 与轨迹
与轨迹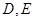 ,求
,求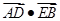 的最小值.
的最小值.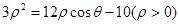
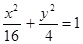 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值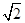 和-1,则点C所对应的实数是
和-1,则点C所对应的实数是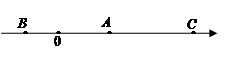

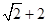

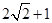
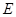 :
: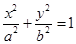 (
(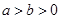 )过点
)过点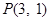 ,其左、右焦点分别为
,其左、右焦点分别为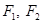 ,且
,且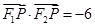 .
.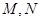 是直线
是直线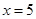 上的两个动点,且
上的两个动点,且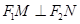 ,则以
,则以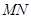 为直径的圆
为直径的圆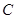 是否过定点?请说明理由.
是否过定点?请说明理由.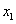 ,
,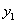 ),B(
),B(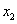 ,
,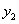 )是函数
)是函数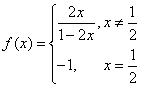 的图象上的任意两点(可以重合),点M在直线
的图象上的任意两点(可以重合),点M在直线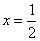 上,且
上,且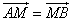 .
.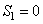 ,当
,当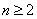 时,
时,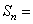
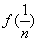 +
+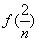 +
+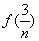 +
+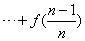 ,求
,求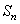 ;
;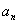 =
=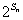 ,
,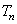 为数列{
为数列{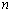 项和,若存在正整数
项和,若存在正整数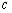 、
、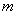 ,
,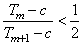 成立,求
成立,求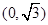 ,曲线C的参数方程为
,曲线C的参数方程为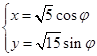 (φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为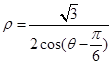 。
。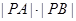 的值。
的值。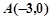 和圆
和圆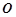 :
: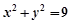 ,
,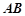 是圆
是圆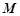 和
和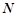 是
是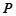 (异于
(异于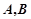 )是圆
)是圆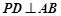 于
于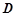 ,
,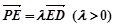 ,直线
,直线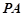 与
与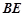 交于
交于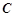 ,则当
,则当 时,
时,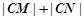 为定值.
为定值.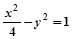 的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )
的两个焦点,P在双曲线上,且满足∠F1PF2=90°,则△PF1F2的面积是( )