题目内容
椭圆 的两个焦点为F1(-c,0),F2(c,0),M是椭圆上的一点,且满足
的两个焦点为F1(-c,0),F2(c,0),M是椭圆上的一点,且满足 .
.(1)求离心率的取值范围;
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为
 ;
;①求此时椭圆G的方程;
②设斜率为k(k≠0)的直线L与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点
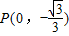 、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
【答案】分析:本题考查的知识点是平面向量的数量积运算,椭圆的标准方程,椭圆的性质及直线与椭圆的关系等知识点,
(1)我们设M(x,y),则易得向量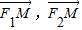 的坐标,由
的坐标,由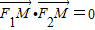 ,结合向量垂直的充要条件,我们即可得到x,y的关系式,又由M又在椭圆上,代入椭圆方程即可得到离心率的取值范围.
,结合向量垂直的充要条件,我们即可得到x,y的关系式,又由M又在椭圆上,代入椭圆方程即可得到离心率的取值范围.
(2)①由(1)的结论,我们易得到离心率e取得最小值时的椭圆方程(含参数),再点N(0,3)到椭圆上的点的最远距离为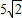 ,我们易得到关于参数的方程,解方程即可得到椭圆的方程.②设出未知直线的方程,然后联立直线方程与椭圆方程,得到一个关于x的一元二次方程,然后使用“设而不求”的方法,结合韦达定理及A、B两点能否关于过点
,我们易得到关于参数的方程,解方程即可得到椭圆的方程.②设出未知直线的方程,然后联立直线方程与椭圆方程,得到一个关于x的一元二次方程,然后使用“设而不求”的方法,结合韦达定理及A、B两点能否关于过点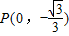 、Q的直线对称构造不等式组,解不等式组即可得到k的取值范围.
、Q的直线对称构造不等式组,解不等式组即可得到k的取值范围.
解答:解:(1)设M(x,y),则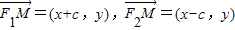
由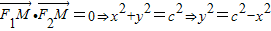 (1分)
(1分)
又M在椭圆上,∴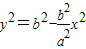 (2分)
(2分)
∴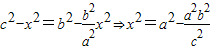 ,(3分)
,(3分)
又0≤x2≤a2∴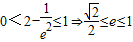 ,(4分)
,(4分)
∵0<e<1,∴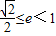 (5分)
(5分)
(2)①当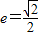 时得椭圆为
时得椭圆为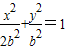
设H(x,y)是椭圆上一点,
则|HN|2=x2+(y-3)2=(2b2-2y2)+(y-3)2=-(y+3)2+2b2+18,(-b≤y≤b)
(6分)
设0<b<3,则-3<-b<0,当y=-b时,|HN|max2=b2+6b+9,,由题意得b2+6b+9=50
∴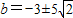 ,与0<b<3矛盾,(7分)
,与0<b<3矛盾,(7分)
设b≥3得-b≤-3,当y=-3时,|HN|max2=2b2+18,,由2b2+18=50得b2=16,(合题薏)
∴椭圆方程是: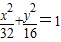 (8分)
(8分)
②.设l:y=kx+m由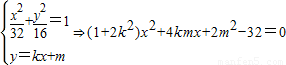
而△>0⇒m2<32k2+16(9分)
又A、B两点关于过点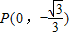 、Q的直线对称
、Q的直线对称
∴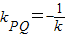 ,设A(x1,y1),B(x2,y2),则
,设A(x1,y1),B(x2,y2),则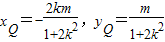 (10分)
(10分)
∴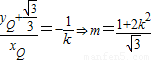 (11分)
(11分)
∴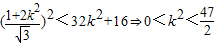 (10分)
(10分)
又k≠0,∴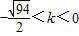 或
或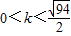 (11分)
(11分)
∴需求的k的取值范围是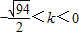 或
或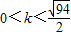 (12分)
(12分)
点评:在处理直线与圆锥曲线的关系类问题时,我们的使用的方法及思路一般有:①联立方程;②设而不求;③韦达定理;④弦长公式等.
(1)我们设M(x,y),则易得向量
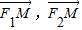 的坐标,由
的坐标,由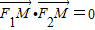 ,结合向量垂直的充要条件,我们即可得到x,y的关系式,又由M又在椭圆上,代入椭圆方程即可得到离心率的取值范围.
,结合向量垂直的充要条件,我们即可得到x,y的关系式,又由M又在椭圆上,代入椭圆方程即可得到离心率的取值范围.(2)①由(1)的结论,我们易得到离心率e取得最小值时的椭圆方程(含参数),再点N(0,3)到椭圆上的点的最远距离为
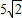 ,我们易得到关于参数的方程,解方程即可得到椭圆的方程.②设出未知直线的方程,然后联立直线方程与椭圆方程,得到一个关于x的一元二次方程,然后使用“设而不求”的方法,结合韦达定理及A、B两点能否关于过点
,我们易得到关于参数的方程,解方程即可得到椭圆的方程.②设出未知直线的方程,然后联立直线方程与椭圆方程,得到一个关于x的一元二次方程,然后使用“设而不求”的方法,结合韦达定理及A、B两点能否关于过点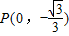 、Q的直线对称构造不等式组,解不等式组即可得到k的取值范围.
、Q的直线对称构造不等式组,解不等式组即可得到k的取值范围.解答:解:(1)设M(x,y),则
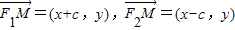
由
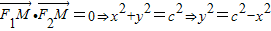 (1分)
(1分)又M在椭圆上,∴
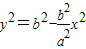 (2分)
(2分)∴
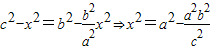 ,(3分)
,(3分)又0≤x2≤a2∴
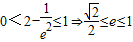 ,(4分)
,(4分)∵0<e<1,∴
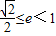 (5分)
(5分)(2)①当
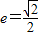 时得椭圆为
时得椭圆为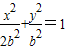
设H(x,y)是椭圆上一点,
则|HN|2=x2+(y-3)2=(2b2-2y2)+(y-3)2=-(y+3)2+2b2+18,(-b≤y≤b)
(6分)
设0<b<3,则-3<-b<0,当y=-b时,|HN|max2=b2+6b+9,,由题意得b2+6b+9=50
∴
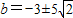 ,与0<b<3矛盾,(7分)
,与0<b<3矛盾,(7分)设b≥3得-b≤-3,当y=-3时,|HN|max2=2b2+18,,由2b2+18=50得b2=16,(合题薏)
∴椭圆方程是:
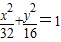 (8分)
(8分)②.设l:y=kx+m由
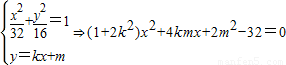
而△>0⇒m2<32k2+16(9分)
又A、B两点关于过点
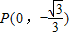 、Q的直线对称
、Q的直线对称∴
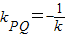 ,设A(x1,y1),B(x2,y2),则
,设A(x1,y1),B(x2,y2),则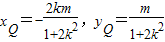 (10分)
(10分)∴
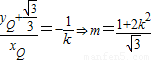 (11分)
(11分)∴
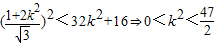 (10分)
(10分)又k≠0,∴
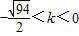 或
或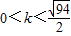 (11分)
(11分)∴需求的k的取值范围是
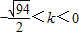 或
或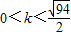 (12分)
(12分)点评:在处理直线与圆锥曲线的关系类问题时,我们的使用的方法及思路一般有:①联立方程;②设而不求;③韦达定理;④弦长公式等.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 的两个焦点为F1、F2,椭圆上一点
的两个焦点为F1、F2,椭圆上一点 满足
满足
 与椭圆恒有两上不同的交点A、B,且
与椭圆恒有两上不同的交点A、B,且 (O是坐标原点),求k的范围。
(O是坐标原点),求k的范围。