题目内容
已知椭圆的两个焦点为F1(-
，0)，F2(
，0)，M是椭圆上一点，若
•
=0，|
|•|
|=8，则该椭圆的方程是（ ）
| 5 |
| 5 |
| MF1 |
| MF2 |
| MF1 |
| MF2 |
分析：由
•
=0，利用数量积可得
⊥
，利用勾股定理可得|
|2+|
|2=(2
)2，
又|
|•|
|=8，联立解出，再利用椭圆的定义可得|
|+|
|=2a，即可得到a．再利用b2=a2-c2即可．
| MF1 |
| MF2 |
| MF1 |
| MF2 |
| MF1 |
| MF2 |
| 5 |
又|
| MF1 |
| MF2 |
| MF1 |
| MF2 |
解答：解：∵
•
=0，∴
⊥
，∴|
|2+|
|2=(2
)2，
又|
|•|
|=8，联立解得|
|=2，|
|=4或|
|=4，|
|=2．
∴|
|+|
|=2a，即2a=2+4，解得a=3．
∴b2=a2-c2=4．
因此椭圆的方程为
+
=1．
故选C．
| MF1 |
| MF2 |
| MF1 |
| MF2 |
| MF1 |
| MF2 |
| 5 |
又|
| MF1 |
| MF2 |
| MF1 |
| MF2 |
| MF1 |
| MF2 |
∴|
| MF1 |
| MF2 |
∴b2=a2-c2=4．
因此椭圆的方程为
| x2 |
| 9 |
| y2 |
| 4 |
故选C．
点评：熟练掌握椭圆的定义及其标准方程、性质、向量垂直与数量积的关系、勾股定理等是解题的关键．
练习册系列答案
相关题目
），（1，0），椭圆的长半轴长为2，则椭圆方程为（ ）
B．
D．
的两个焦点为F1、F2，椭圆上一点
满足
与椭圆恒有两上不同的交点A、B，且
（O是坐标原点），求k的范围。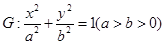
的两个焦点为
、
，点
在椭圆G上，且
，且
，斜率为1的直线
与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3,2）.
的面积.
，
，
是椭圆上一点，
，
，则该椭圆的方程是( ) 
B、
C、
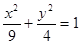D、