题目内容
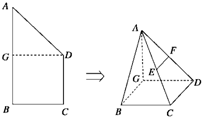 如图,在直角梯形ABCD中,∠B=90°,DC∥AB,BC=CD=
如图,在直角梯形ABCD中,∠B=90°,DC∥AB,BC=CD=| 1 | 2 |
(1)若E,F分别为线段AC,AD的中点,求证:EF∥平面ABG;
(2)求三棱锥C-ABD的体积.
分析:(1)利用三角形的中位线定理和线面平行的判定定理即可证明;
(2)先证明AG⊥底面BCD,再利用V三棱锥C-ABD=V三棱锥A-BCD即可求出.
(2)先证明AG⊥底面BCD,再利用V三棱锥C-ABD=V三棱锥A-BCD即可求出.
解答:解(1)∵折叠前后CD、BG的位置关系不变,∴CD∥BG.
∵在△ACD中,E、F分别为AC、BD的中点,∴EF∥CD.
∴EF∥BG.
又∵EF?平面ABG,BG?平面ABG,
∴EF∥平面ABG.
(2)∵BC=CD=
AB=2,G为线段AB的中点,∴CD=BG,
又∵∠B=90°,CD∥BG,∴四边形BCDG是一个正方形,∴BG⊥DG,AG⊥DG,
折叠后仍然成立,
∵平面ADG⊥平面BCDG,∴AG⊥平面BCDG.
∴V三棱锥C-ABD=V三棱锥A-BCD=
AG×S△BCD=
×2×
×2×2=
.
∵在△ACD中,E、F分别为AC、BD的中点,∴EF∥CD.
∴EF∥BG.
又∵EF?平面ABG,BG?平面ABG,
∴EF∥平面ABG.
(2)∵BC=CD=
| 1 |
| 2 |
又∵∠B=90°,CD∥BG,∴四边形BCDG是一个正方形,∴BG⊥DG,AG⊥DG,
折叠后仍然成立,
∵平面ADG⊥平面BCDG,∴AG⊥平面BCDG.
∴V三棱锥C-ABD=V三棱锥A-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
点评:熟练掌握三角形的中位线定理、线面平行的判定定理及面面、线面垂直的判定和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则