题目内容
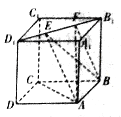
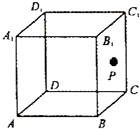
【题目】如图，正四面体ABCD的顶点C在平面α内，且直线BC与平面α所成角为15°，顶点B在平面α上的射影为点O，当顶点A与点O的距离最大时，直线CD与平面α所成角的正弦值为 ．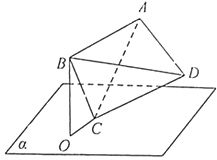 
【答案】
【解析】解：当四边形ABOC为平面四边形时，点A到点O的距离最大．
此时平面ABOC⊥平面α，过D作DN⊥平面ABOC，垂足为N，
则N为正三角形ABC的中心．
设正四面体的边长为1，则CN= 
CP= 
，
∵∠BCO=15°，∠BCP=30°，∴∠OCN=45°，
∴N到平面α的距离d= 
= ．
过D作DM⊥平面α，垂足为M，则DM=d= ，
∴直线CD与平面α所成角的正弦值为 
= ．
故答案为： 
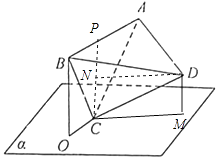
当A，B，O，C四点共面时，|OA|最大，过D作平面ABOC的垂线DN，则垂足为△ABC的中心，求出N到平面α的距离d，则直线CD与平面α所成角的正弦值为 
．
练习册系列答案
相关题目
【题目】若学生
一天学习数学超过两个小时的概率为
（每天是相互独立没有影响的），一周内至少有四天每天学习数学超过两个小时，就说该生本周数学学习是投入的.
（Ⅰ）①设学生本周一天学习数学超过两个小时的天数为
求
的分布列与数学期望
②求学生本周数学学习投入的概率.
（Ⅱ）为了研究学生学习数学的投入程度和本周数学周练成绩的关系，随机在年级中抽取了
名学生进行调查，所得数据如下表所示：
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”？
附：
|
|
|
|
|
|
|
|
|
|
| 10.828 |
