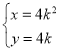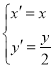题目内容
【题目】已知抛物线Γ的准线方程为
.焦点为
.
（1）求证：抛物线Γ上任意一点
的坐标
都满足方程：
（2）请求出抛物线Γ的对称性和范围，并运用以上方程证明你的结论；
（3）设垂直于
轴的直线与抛物线交于
两点，求线段
的中点
的轨迹方程.
【答案】（1）证明见解析（2）关于
对称
.证明见解析（3）
（在抛物线内）
【解析】
（1）由抛物线的定义可得|PF|＝d（d为P到准线的距离），运用两点的距离公式和点到直线的距离公式，化简可得所求轨迹方程；
（2）由抛物线的方程的特点，考虑点关于直线y＝x的对称点的特征和对称轴与准线和抛物线的交点的关系，以及直线和抛物线相切的特点，可得所求范围；
（3）设垂直于x轴的直线为x＝t，代入抛物线的方程x2﹣2xy+y2﹣8x﹣8y＝0，运用韦达定理和中点坐标公式，以及参数方程化为普通方程可得所求轨迹方程．
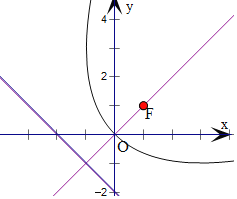
（1）抛物线Γ的准线方程为x+y+2＝0，焦点为F（1，1），
抛物线Γ上任意一点P的坐标（x，y），由抛物线的定义可得|PF|＝d（d为P到准线的距离），即为
，两边平方化简可得x2﹣2xy+y2﹣8x﹣8y＝0；
（2）抛物线关于y＝x对称，顶点为（0，0），范围为x≥﹣1，y≥﹣1，
由方程x2﹣2xy+y2﹣8x﹣8y＝0，
设抛物线上任一点（x，y）关于直线y＝x对称的点为（y，x），满足原方程，
则抛物线关于直线y＝x对称；
由直线y﹣1＝x﹣1即y＝x，联立x+y+2＝0，解得x＝y＝﹣1，
可得抛物线的顶点为（0，0）；
由x＝﹣1和x2﹣2xy+y2﹣8x﹣8y＝0联立可得切点为（﹣1，3），
同样由y＝﹣1和x2﹣2xy+y2﹣8x﹣8y＝0联立可得切点为（3，﹣1），
可得抛物线的范围为x≥﹣1，y≥﹣1；
（3）设垂直于x轴的直线为x＝t，代入抛物线的方程x2﹣2xy+y2﹣8x﹣8y＝0，
可得t2﹣（2t+8）y+ t2﹣8t＝0，
设A（t，y1），B（t，y2），可得y1+y2＝2t+8，
则AB的中点为（t，t+4），
则AB的中点的轨迹方程为直线y＝x+4（在抛物线内）．
