题目内容
如图,在△OAB中,已知P为线段AB上的一点,
=x•
+y•
.
(1)若
=
,求x,y的值;
(2)若
=3
,|
|=4,|
|=2,且
与
的夹角为60°时,求
•
的值.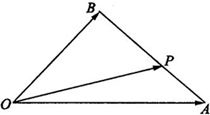
| OP |
| OA |
| OB |
(1)若
| BP |
| PA |
(2)若
| BP |
| PA |
| OA |
| OB |
| OA |
| OB |
| OP |
| AB |

(1)∵
=
,
∴
+
=
+
,即2
=
+
,
∴
=
+
,即x=
,y=
(2)∵
=3
,
∴
+
=3
+3
,即4
=
+3
∴
=
+
∴x=
,y=
•
=(
+
)•(
-
)
=
•
-
•
+
•
=
×22-
×42+
×4×2×
=-9
| BP |
| PA |
∴
| BO |
| OP |
| PO |
| OA |
| OP |
| OB |
| OA |
∴
| OP |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵
| BP |
| PA |
∴
| BO |
| OP |
| PO |
| OA |
| OP |
| OB |
| OA |
∴
| OP |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
∴x=
| 3 |
| 4 |
| 1 |
| 4 |
| OP |
| AB |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
| OB |
| OA |
=
| 1 |
| 4 |
| OB |
| OB |
| 3 |
| 4 |
| OA |
| OA |
| 1 |
| 2 |
| OA |
| OB |
=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
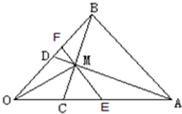 如图,在△OAB中,
如图,在△OAB中, (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且 如图,在△OAB中,已知
如图,在△OAB中,已知 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=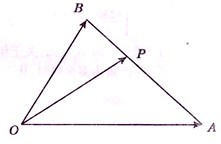 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|