题目内容
已知定义域为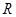 的奇函数
的奇函数 .当
.当 时,
时,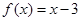 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
A
解析试题分析:根据 为奇函数,且当
为奇函数,且当 时,
时,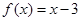 ,可作出该函数的图像如下
,可作出该函数的图像如下
由图可知,当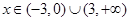 时,
时, ,当
,当 时,
时, ,所以
,所以 的解集为
的解集为 ,故选A.
,故选A.
考点:1.函数的奇偶性;2.一次函数的图像与性质;3.不等式.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知减函数 是定义在
是定义在 上的奇函数,则不等式
上的奇函数,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
在定义域内既是奇函数又为增函数的是( )
A. | B. | C. | D. |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则 =( )
=( )
| A.2 | B.1 | C.0 | D.-2 |
已知 是定义域为R的奇函数,当x≤0时,
是定义域为R的奇函数,当x≤0时, ,则不等式
,则不等式 的解集是( )
的解集是( )
A.( 5,5) 5,5) | B.( 1,1) 1,1) |
C.( 5,+ 5,+ ) ) | D.( l,+ l,+ ) ) |
已知函数 是
是 上的减函数,那么实数
上的减函数,那么实数 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.(0, ) ) | C. | D. |
 切直线
切直线 于
于 点,射线
点,射线 从
从 出发绕着
出发绕着 ,旋转过程中
,旋转过程中 ,记
,记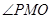 为
为 ,弓形
,弓形 的面积
的面积 ,那么
,那么 的大致图象是 ( )
的大致图象是 ( )

 的图象的大致形状是( )
的图象的大致形状是( )