题目内容
如图,四棱锥P—ABCD的底面是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点,又二面角P-CD-B为45°.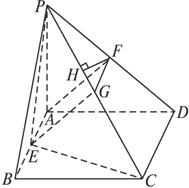
(1)求证:AF∥平面PEC;
(2)求证:平面PEC⊥平面PCD;
(3)设AD=2,CD=2![]() ,求点A到平面PEC的距离.
,求点A到平面PEC的距离.
剖析:对问题(1),关键是证明AF与平面PEC内的一条直线平行,为此可取PC的中点G,论证AF∥EG;对问题(2),可转化为证明线面垂直;对问题(3),可转化为求点F到平面PEC的距离,进而可以充分运用(2)的结论.
(1)证明:取PC的中点G,连结EG、FG.
∵F是PD的中点,
∴FG∥CD且FG=![]() CD.
CD.
而AE∥CD且AE=![]() CD,
CD,
∴EA∥GF且EA=GF,
故四边形EGFA是平行四边形,从而EG∥AF.
又AF![]() 平面PEC,EG
平面PEC,EG![]() 平面PEC,
平面PEC,
∴AF∥平面PEC.
(2)证明:∵PA⊥平面ABCD,
∴AD是PD在平面ABCD上的射影.
又CD⊥AD,
∴CD⊥PD,∠PDA就是二面角P-CD-B的平面角.
∴∠ADP=45°,则AF⊥PD.
又AF⊥CD,PD∩CD=D,
∴AF⊥平面PCD.
由(1),EG∥AF,
∴EG⊥平面PCD.
而EG![]() 平面PEC,
平面PEC,
∴平面PEC⊥平面PCD.
(3)解:过F作FH⊥PC交PC于点H,又平面PEC⊥平面PCD,则FH⊥平面PEC,
∴FH为点F到平面PEC的距离,而AF∥平面PEC,故FH等于点A到平面PEC的距离.
在△PFH与△PCD中,
∵∠FHP=∠CDP=90°,∠FPC为公共角,
∴△PFH∽△PCD,![]() =
=![]() .
.
∵AD=2,CD=2![]() ,PF=
,PF=![]() ,PC=
,PC=![]() =4,
=4,
∴FH=![]() ·2
·2![]() =1.
=1.
∴点A到平面PEC的距离为1.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=