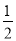题目内容
1.设方程x4-15x3+kx2+175x-1992=0的四个根中有两根的乘积为24,求k的值.分析 不妨设方程x4-15x3+kx2+175x-1992=0的四个根为x1,x2,x3,x4,且x1x2=24;从而由x4-15x3+kx2+175x-1992=(x-x1)(x-x2)(x-x3)(x-x4)=(x2-(x1+x2)x+x1x2)(x2-(x3+x4)x+x3x4)可得x1x2x3x4=-1992,x1+x2+x3+x4=15,83(x1+x2)-24(x3+x4)=175,从而求k.
解答 解:不妨设方程x4-15x3+kx2+175x-1992=0的四个根为x1,x2,x3,x4,且x1x2=24;
则x4-15x3+kx2+175x-1992=(x-x1)(x-x2)(x-x3)(x-x4)
=(x2-(x1+x2)x+x1x2)(x2-(x3+x4)x+x3x4);
故x1x2x3x4=-1992,
故x3x4=-$\frac{1992}{24}$=-83;
故(x2-(x1+x2)x+24)(x2-(x3+x4)x-83)
则x1+x2+x3+x4=15,
83(x1+x2)-24(x3+x4)=175,
联立方程解得,
x1+x2=5,x3+x4=10;
故k=(x1+x2)(x3+x4)+24-83=50+24-83=-9.
点评 本题考查了多项式的化简与运算,属于中档题.

练习册系列答案
相关题目
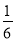 B.
B.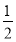
 D.
D.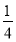
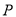 是
是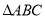 所在平面内一点且
所在平面内一点且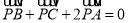 ,现将一粒黄豆随机撕在
,现将一粒黄豆随机撕在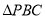 内的概率是( )
内的概率是( )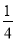 B.
B.
 D.
D.