题目内容
5.已知点A是半径为1的⊙O外一点,且AO=2,若M,N是⊙O一条直径的两个端点,则$\overrightarrow{AM}$$•\overrightarrow{AN}$=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先由题意画出图象,利用向量的加法法则得:$\overrightarrow{AM}$=$\overrightarrow{AO}+\overrightarrow{OM}$、$\overrightarrow{AN}$=$\overrightarrow{AO}+\overrightarrow{ON}$,由向量的数量积运算和条件求出$\overrightarrow{AM}•\overrightarrow{AN}$的值.
解答 解: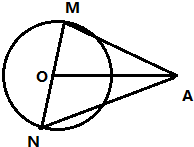 如右图:0A=2,OM=ON=1,
如右图:0A=2,OM=ON=1,
∵$\overrightarrow{AM}$=$\overrightarrow{AO}+\overrightarrow{OM}$,$\overrightarrow{AN}$=$\overrightarrow{AO}+\overrightarrow{ON}$,
∴$\overrightarrow{AM}•\overrightarrow{AN}$=($\overrightarrow{AO}+\overrightarrow{OM}$)•($\overrightarrow{AO}+\overrightarrow{ON}$)
=${\overrightarrow{AO}}^{2}$+$\overrightarrow{AO}•\overrightarrow{ON}$+$\overrightarrow{OM}•\overrightarrow{AO}$+$\overrightarrow{OM}•\overrightarrow{ON}$
=${\overrightarrow{AO}}^{2}$+$\overrightarrow{AO}•(\overrightarrow{ON}+\overrightarrow{OM})$+$\overrightarrow{OM}•\overrightarrow{ON}$
=4+0-1=3,
故选:C.
点评 本题考查向量的数量积运算,以及向量的加法法则,属于中档题.

| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 对任意
对任意 ,
, 满足
满足 ,且
,且 ,则
,则 等于( )
等于( )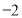 B.
B.
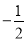 D.
D.