题目内容
在等差数列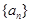 中,若任意两个不等的正整数
中,若任意两个不等的正整数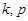 ,都有
,都有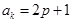 ,
,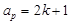 ,设数列
,设数列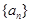 的前
的前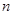 项和为
项和为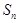 ,若
,若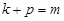 ,则
,则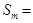 (结果用
(结果用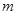 表示)。
表示)。
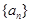 中,若任意两个不等的正整数
中,若任意两个不等的正整数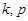 ,都有
,都有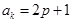 ,
,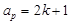 ,设数列
,设数列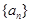 的前
的前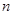 项和为
项和为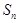 ,若
,若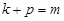 ,则
,则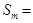 (结果用
(结果用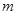 表示)。
表示)。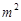
解:设公差为d,∵ak=2p+1=a1+(k-1)d (1),ap=2k+1=a1+(p-1)d (2),
由(1)-(2)可得d=-2.
故有 a1+(k-1)(-2)=a1+(p-1)(-2),∴a1-2(k-1)=2p+1,∴a1=2p+1+2(k-1)=2(p+k)-1=2m-1.
Sm=ma1+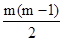 d=m(2m-1)+
d=m(2m-1)+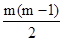 •(-2)=m2,故答案为 m2
•(-2)=m2,故答案为 m2
由(1)-(2)可得d=-2.
故有 a1+(k-1)(-2)=a1+(p-1)(-2),∴a1-2(k-1)=2p+1,∴a1=2p+1+2(k-1)=2(p+k)-1=2m-1.
Sm=ma1+
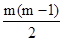 d=m(2m-1)+
d=m(2m-1)+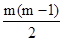 •(-2)=m2,故答案为 m2
•(-2)=m2,故答案为 m2
练习册系列答案
相关题目
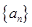 满足
满足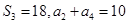 。
。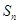 的最大值;
的最大值;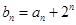 ,求数列
,求数列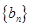 的其前
的其前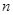 项和
项和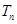 .
.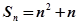 ,那么它的通项公式为an="_________" .
,那么它的通项公式为an="_________" .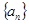 中,
中,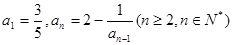 ,数列
,数列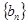 满足
满足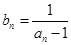 .
.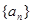 的公差为2,若
的公差为2,若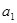 ,
,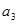 ,
,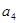 成等比数列,则
成等比数列,则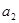 等于( )
等于( ) B
B  C
C  D
D 
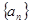 中,
中,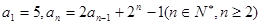 ,若存在实数
,若存在实数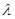 ,使得数列
,使得数列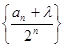 为等差数列,则
为等差数列,则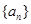 中,
中,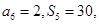 则
则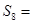 ( )
( )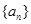 中,
中,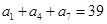 ,
,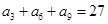 ,则数列
,则数列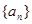 中,已知
中,已知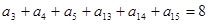 ,则
,则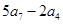 = .
= .