题目内容
已知数列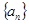 中,
中,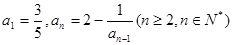 ,数列
,数列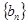 满足
满足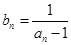 .
.
(1)求证:数列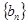 是等差数列;
是等差数列;
(2)求数列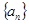 中的最大项和最小项,并说明理由.
中的最大项和最小项,并说明理由.
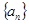 中,
中,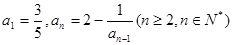 ,数列
,数列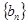 满足
满足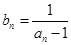 .
.(1)求证:数列
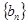 是等差数列;
是等差数列;(2)求数列
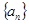 中的最大项和最小项,并说明理由.
中的最大项和最小项,并说明理由.解:(1)证明略
(2)当n=3时,an取得最小值-1; 当n=4时,an取得最大值3
(2)当n=3时,an取得最小值-1; 当n=4时,an取得最大值3
本试题主要是考查了数列的定义以及数列单调性的证明。
(1)因为an=2-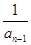 (n≥2,n∈N*),bn=
(n≥2,n∈N*),bn=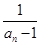 .所以当n≥2时,bn-bn-1=
.所以当n≥2时,bn-bn-1=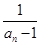 -
-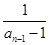
=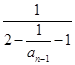 -
-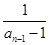 =
=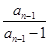 -
-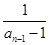 =1. 又b1=
=1. 又b1= =-
=-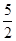 .
.
得到数列是等差数列,求解通项公式。
(2)由(1)知, bn=n-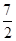 ,则an=1+
,则an=1+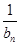 =1+
=1+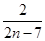 .
.
设函数f(x)=1+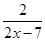 阿,易知f(x)在区间 (-∞,
阿,易知f(x)在区间 (-∞,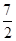 )和(
)和(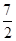 ,+∞)内为减函数,从而得到结论。
,+∞)内为减函数,从而得到结论。
(1)因为an=2-
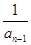 (n≥2,n∈N*),bn=
(n≥2,n∈N*),bn=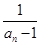 .所以当n≥2时,bn-bn-1=
.所以当n≥2时,bn-bn-1=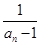 -
-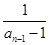
=
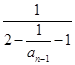 -
-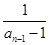 =
=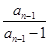 -
-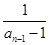 =1. 又b1=
=1. 又b1= =-
=-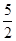 .
.得到数列是等差数列,求解通项公式。
(2)由(1)知, bn=n-
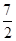 ,则an=1+
,则an=1+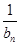 =1+
=1+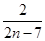 .
.设函数f(x)=1+
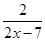 阿,易知f(x)在区间 (-∞,
阿,易知f(x)在区间 (-∞,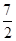 )和(
)和(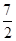 ,+∞)内为减函数,从而得到结论。
,+∞)内为减函数,从而得到结论。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
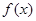 定义在区间
定义在区间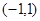 上,
上,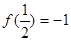 ,且当
,且当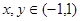 时,
时,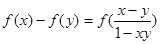 .又数列
.又数列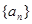 满足
满足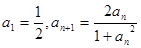 .
.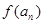 的表达式;
的表达式;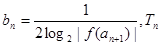 为数列
为数列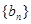 的前
的前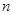 项和,若
项和,若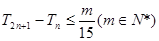 对
对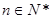 恒成立,求
恒成立,求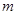 的最小值.
的最小值.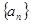 中,
中,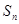 是其前
是其前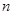 项和,
项和,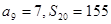 ,求:
,求: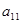 及
及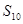 .
.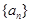 中,若任意两个不等的正整数
中,若任意两个不等的正整数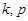 ,都有
,都有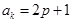 ,
,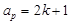 ,设数列
,设数列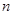 项和为
项和为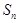 ,若
,若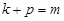 ,则
,则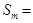 (结果用
(结果用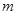 表示)。
表示)。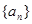 的前
的前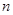 项和记为
项和记为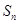 ,
,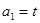 ,
,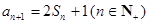 .
.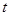 为何值时,数列
为何值时,数列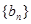 的前
的前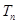 有最大值,且
有最大值,且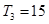 ,又
,又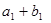 ,
,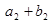 ,
,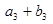 成等比数列,求
成等比数列,求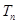 .
.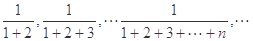 的前
的前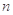 项和为 ( )
项和为 ( )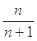
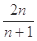
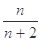
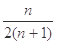
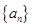 的
的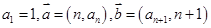 ,且
,且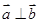 ,则
,则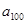 = ( )
= ( )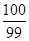
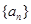 中,若
中,若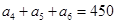 ,则
,则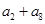 的值为 .
的值为 .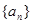 的前
的前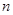 项和为
项和为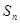 ,且
,且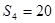 ,
,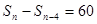 ,
,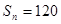 ,则
,则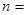 .
.