题目内容
【题目】椭圆 
=1上有一点M（﹣4， 
）在抛物线y2=2px（p＞0）的准线l上，抛物线的焦点也是椭圆焦点．
（1）求椭圆的标准方程；
（2）若点N在抛物线上，过N作准线l的垂线，垂足为Q，求|MN|+|NQ|的最小值．
【答案】
（1）解：∵ 
=1上的点M在抛物线y2=2px（p＞0）的准线l上，抛物线的焦点也是椭圆焦点．
∴c=﹣4，p=8…①
∵M（﹣4， 
）在椭圆上，∴ 
…②
又∵a2=b2+c2…③
∴由①②③解得：a=5、b=3，
∴椭圆为 
；
由p=8得抛物线为y2=16x
（2）解：设椭圆焦点为F（4，0），由椭圆定义得|NQ|=|NF|，
∴|MN|+|NQ|=|MN|+|NF|≥|MF|= 
，即为所求的最小值．
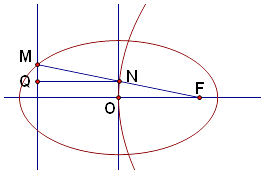
【解析】（1）由题意求得c=﹣4，得到p=8，再由点M（﹣4， ）在椭圆上，结合隐含条件求得a，b的值，则椭圆方程和抛物线方程可求；（2）由题意画出图形，由抛物线定义把|MN|+|NQ|的最小值转化为|MF|求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
