设不等式组$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\end{array}\right.$表示的区域为A.不等式组$\left\{\begin{array}{l}{2x+y-6≥0}\\{2x-3y≥0}\end{array}\right.$表示的区域为B．(1)在区域A中任取一点.求点(x.y)∈B的概率,(2)若x.y分别表示甲乙两人各掷一� 题目和参考答案——青夏教育精英家教网—

题目内容

3．设不等式组$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\end{array}\right.$表示的区域为A，不等式组$\left\{\begin{array}{l}{2x+y-6≥0}\\{2x-3y≥0}\end{array}\right.$表示的区域为B．
（1）在区域A中任取一点（x，y），求点（x，y），求点（x，y）∈B的概率；
（2）若x，y分别表示甲乙两人各掷一次骰子所得的点数，求点（x，y）在区域B中的概率．

分析（1）求出区域A的面积和区域B的面积，代入几何概型概率计算公式，可得答案．
（2）求出甲、乙两人各掷一次骰子所得的点数的所有情况，及满足点（x，y）在区域B中的情况，代入古典概型概率计算公式，可得答案．

解答解：（1）设区域A中的点（x，y）∈B为事件M，…（1分）
点（x，y）落在区域内任一点是等可能的…（2分）
∵不等式组$\left\{\begin{array}{l}0≤x≤6\\ 0≤y≤6\end{array}\right.$表示区域A，
∴区域A的面积为S₁=36，
又∵不等式组$\left\{\begin{array}{l}2x+y-6≥0\\ 2x-3y≥0\\ 0≤x≤6\\ 0≤y≤6\end{array}\right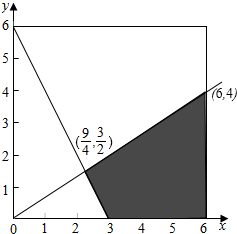.$表示的区域为区域A中任取一点（x，y）∈B．

∴区域B的面积为S₂=$\frac{1}{2}×6×4$-$\frac{1}{2}$×3×$\frac{3}{2}$=$\frac{39}{4}$，…（4分）
∴P（M）=$\frac{\frac{39}{4}}{36}$=$\frac{13}{48}$．…（6分）
答：点（x，y）∈B的概率为$\frac{13}{48}$…（7分）
（2）设点（x，y）在区域B为事件N，点（x，y）落在区域内任一点是等可能的…（8分）
甲、乙两人各掷一次骰子所得的点（x，y）的个数为36个，…（9分）
其中在区域B中的点（x，y）有（3，1），（3，2），
（4，1），（4，2），（5，1），（5，2），（5，3），（6，1），（6，2），（6，3），（6，4）共11个，…（12分）
故P（N）=$\frac{11}{36}$，
答：点（x，y）在区域B中的概率为$\frac{11}{36}$…（14分）