题目内容
如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为 ( )
A. | B. | C. | D. |
A
解析试题分析:设半径为 ,则有
,则有 ,所以
,所以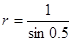 ,故弧长
,故弧长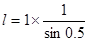 =
=
考点:弧长公式
点评:本题考查弧长公式,求解本题的关键是利用弦心距,弦长的一半,半径构成一个直角三角形求半径,熟练记忆弧长公式也是正确解题的关键.

练习册系列答案
相关题目
若函数 的图象关于直线
的图象关于直线 对称,则
对称,则 可以为( )
可以为( )
A. | B.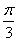 | C. | D. |
如果角θ的终边经过点 那么tanθ的值是( )
那么tanθ的值是( )
A. | B. | C. | D. |
若2弧度的圆心角所对的弧长为4cm,则这个圆心角所夹的扇形的面积是( )
| A.4 cm2 | B.2 cm2 | C.4πcm2 | D.2πcm2 |
为了使函数y= sinωx(ω>0)在区间[0,1]是至少出现50次最大值,则ω的最小值是 ( )
| A.98π | B.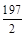 π π |
C.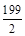 π π | D.100π |
为了使函数y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值,则ω的最小值是( ).
| A.98π | B.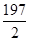 π π | C.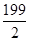 π π | D.100π |
设 ,则
,则
A. | B. | C. | D. |
如图所示,是函数y=Asin(ωx+φ)(A>0,ω>0, -p<φ<0)的简图,则振幅、周期、初相分别是 ( )
A.2, ,? ,? | B.2, ,? ,? |
C.4, ,? ,? | D.2, ,? ,? |
 -2x)的单调增区间是[
-2x)的单调增区间是[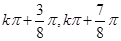 ],kÎZ
],kÎZ
 sin(wx)的最小正周期为4p,则w=
sin(wx)的最小正周期为4p,则w=