题目内容
为了使函数y= sinωx(ω>0)在区间[0,1]是至少出现50次最大值,则ω的最小值是 ( )
| A.98π | B.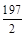 π π |
C.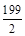 π π | D.100π |
B
解析试题分析:因为,使y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值,
所以,49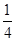 ×T≤1,即
×T≤1,即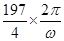 ≤1,
≤1,
所以,ω≥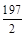 π,故选B.
π,故选B.
考点:本题主要考查正弦型函数的图象和性质。
点评:简单题,根据正弦型函数的图象和性质,确定 应满足的条件。
应满足的条件。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图是函数 在区间上
在区间上 的图像,为了得到这个函数的图象,只要将
的图像,为了得到这个函数的图象,只要将 的图象上所有的点
的图象上所有的点
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
设 ,则
,则 是 ( )
是 ( )
A.周期为 的奇函数 的奇函数 | B.周期为 的偶函数 的偶函数 | C.周期为 的奇函数 的奇函数 | D.周期为 的偶函数 的偶函数 |
在(0,2π)内,使sinx>cosx成立的x的取值范围是( )
A.( , , )∪(π, )∪(π, ) ) | B.( ,π) ,π) |
C.( , , ) ) | D.( ,π)∪( ,π)∪( , , ) ) |
如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为 ( )
A. | B. | C. | D. |
要得到 的图象,只需将
的图象,只需将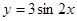 的图象( )
的图象( )
A.左移 个单位 个单位 | B.右移 个单位. 个单位. | C.左移 个单位 个单位 | D.右移 个单位 个单位 |
已知函数 ,若
,若 ,则
,则 与
与 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D.大小与a、 有关 有关 |
 最小值是 ( )
最小值是 ( )
| A.-1 | B. | C. | D.1 |
 ,则
,则 的值为( )
的值为( )
A.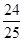 | B.-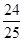 | C. | D. |