题目内容
下列6个命题中正确命题个数是( )
(1)第一象限角是锐角
(2)y=sin( -2x)的单调增区间是[
-2x)的单调增区间是[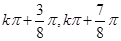 ],kÎZ
],kÎZ
(3)角a终边经过点(a,a)(a¹0)时,sina+cosa=
(4)若y= sin(wx)的最小正周期为4p,则w=
sin(wx)的最小正周期为4p,则w=
(5)若cos(a+b)=-1,则sin(2a+b)+sinb=0
(6)若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期函数
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析:361°是第一象限角,但不是锐角,故(1)第一象限角是锐角错误;∵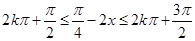 ,∴
,∴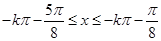 ,当k=-1时,单调增区间为[
,当k=-1时,单调增区间为[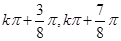 ],kÎZ,故(2)正确;∵角a终边经过点(a,a)时,当a=-1时,sina+cosa=-
],kÎZ,故(2)正确;∵角a终边经过点(a,a)时,当a=-1时,sina+cosa=- ,故(3)角a终边经过点(a,a)时,sina+cosa=
,故(3)角a终边经过点(a,a)时,sina+cosa= 错误;若y=
错误;若y= sin(ωx)的最小正周期为4π,则ω=±
sin(ωx)的最小正周期为4π,则ω=± ,故(4)若y=
,故(4)若y= sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω= 错误;若cos(α+β)=-1,则sin(α+β)=0,则sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α]=2sin(α+β)cos(α+β)=0,故(5)正确;若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期为2的周期函数,故(6)正确;故正确的命题有(2)、(5)、(6),故选C
错误;若cos(α+β)=-1,则sin(α+β)=0,则sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α]=2sin(α+β)cos(α+β)=0,故(5)正确;若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期为2的周期函数,故(6)正确;故正确的命题有(2)、(5)、(6),故选C
考点:本题考查了三角函数的性质
点评:命题的真假判断与应用,函数的周期性,平行向量与共线向量,终边相同的角,象限角、轴线角,三角函数的周期性及其求法,属于基础题型,真正理解和掌握相关的定义是解答本题的关键.

 阅读快车系列答案
阅读快车系列答案函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. |
C. | D. |
函数 的图象( )
的图象( )
| A.关于原点对称 | B.关于点(- ,0)对称 ,0)对称 |
| C.关于y轴对称 | D.关于直线x= 对称 对称 |
设 ,则
,则 是 ( )
是 ( )
A.周期为 的奇函数 的奇函数 | B.周期为 的偶函数 的偶函数 | C.周期为 的奇函数 的奇函数 | D.周期为 的偶函数 的偶函数 |
若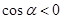 且
且 ,则
,则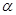 是( )
是( )
| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
在(0,2π)内,使sinx>cosx成立的x的取值范围是( )
A.( , , )∪(π, )∪(π, ) ) | B.( ,π) ,π) |
C.( , , ) ) | D.( ,π)∪( ,π)∪( , , ) ) |
如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为 ( )
A. | B. | C. | D. |
已知函数 ,若
,若 ,则
,则 与
与 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D.大小与a、 有关 有关 |
已知函数y=2sin(2x+ )(|
)(| |<
|<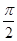 )的图象经过点(0,1),则该函数的一条对称轴方程为
)的图象经过点(0,1),则该函数的一条对称轴方程为
A.x= | B.x= | C.x=- | D.x=- |