题目内容
(本小题满分12分)
已知函数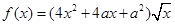 ,其中
,其中 .
.
(1)当 时,求
时,求 的单调递增区间;
的单调递增区间;
(2)若 在区间
在区间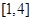 上的最小值为8,求
上的最小值为8,求 的值.
的值.
(1)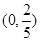 和
和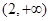 ,(2)
,(2)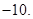
解析试题分析:(1)利用导数求函数单调区间,首先确定定义域: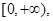 然后对函数求导,在定义域内求导函数的零点:
然后对函数求导,在定义域内求导函数的零点: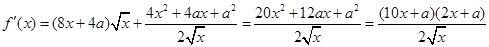 ,当
,当 时,
时,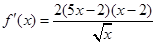 ,由
,由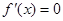 得
得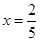 或
或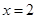 ,列表分析得单调增区间:
,列表分析得单调增区间: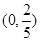 和
和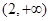 ,(2)已知函数最值,求参数,解题思路还是从求最值出发.由(1)知,
,(2)已知函数最值,求参数,解题思路还是从求最值出发.由(1)知,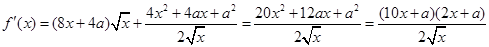 ,所以导函数的零点为
,所以导函数的零点为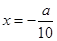 或
或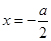 ,列表分析可得:函数增区间为
,列表分析可得:函数增区间为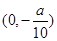 和
和 ,减区间为
,减区间为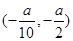 .由于
.由于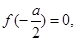 所以
所以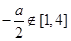 ,当
,当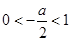 时,
时,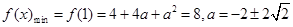 ,(舍),当
,(舍),当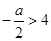 时,
时,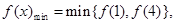 由于
由于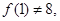 所以
所以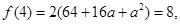 且
且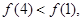 解得
解得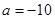 或
或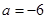 (舍),当
(舍),当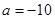 时,
时, 在
在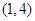 上单调递减,满足题意,综上
上单调递减,满足题意,综上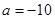 .
.
试题解析:(1)定义域: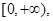 而
而 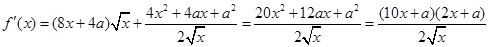 ,当
,当 时,
时,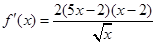 ,由
,由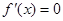 得
得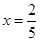 或
或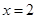 ,列表:
,列表:
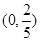
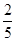
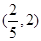
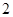
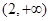
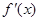



 练习册系列答案
练习册系列答案
启文引路系列答案
南方新中考系列答案
知识与能力训练系列答案
名校作业课时精练系列答案
六月冲刺系列答案

课时同步导练系列答案
夺分王系列答案
助学读本系列答案
指南针导学探究系列答案
相关题目
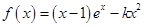 (其中
(其中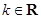 ).
).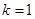 时,求函数
时,求函数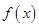 的单调区间;
的单调区间;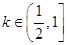 时,求函数
时,求函数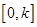 上的最大值
上的最大值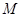 .
.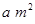 ,
,
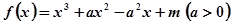
 的单调增区间;
的单调增区间;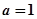 时,函数
时,函数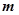 的取值范围.
的取值范围.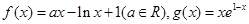 。
。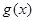 在区间
在区间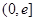 上的值域;
上的值域;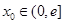 ,在区间
,在区间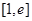 上都存在两个不同的
上都存在两个不同的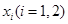 ,使得
,使得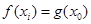 成立.若存在,求出a的取值范围;若不存在,请说明理由.
成立.若存在,求出a的取值范围;若不存在,请说明理由.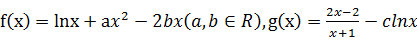 .
.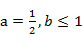 时,
时,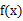 与
与 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 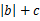 的最小值。
的最小值。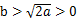 时,求证:存在
时,求证:存在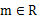 ,使
,使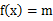 的三个不同的实数解
的三个不同的实数解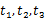 ,且对任意
,且对任意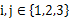 且
且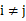 都有
都有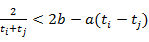 .
. ,其中
,其中 .
. 的定义域
的定义域 (用区间表示);
(用区间表示); ,求
,求 的
的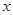 的集合(用区间表示).
的集合(用区间表示).
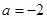 ,求证:函数
,求证:函数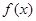 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;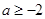 时,求函数
时,求函数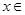 [l,e],使得
[l,e],使得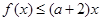 成立,求实数
成立,求实数 的取值范围.
的取值范围.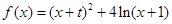 的图象在点
的图象在点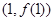 处的切线垂直于
处的切线垂直于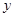 轴.
轴.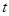 的值;
的值;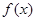 的极值.
的极值.