题目内容
1.设a,b,c∈R+,且ab+bc+ca=108,则$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$的最小值是18.分析 $\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$=$\frac{(ab)^{2}+(bc)^{2}+(ca)^{2}}{abc}$≥$\frac{a{b}^{2}c+{a}^{2}bc+ab{c}^{2}}{abc}$=a+b+c,再证明a+b+c≥18,即可求出$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$的最小值.
解答 解:$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$=$\frac{(ab)^{2}+(bc)^{2}+(ca)^{2}}{abc}$≥$\frac{a{b}^{2}c+{a}^{2}bc+ab{c}^{2}}{abc}$=a+b+c,
∵(a+b+c)2≥3(ab+bc+ca)=324,
∴a+b+c≥18,
∴$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$≥18,
∴$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$的最小值是18.
故答案为:18.
点评 本题考查$\frac{ab}{c}+\frac{bc}{a}+\frac{ca}{b}$的最小值,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
9.已知有穷数列5,7,9,…,2n+7(n为偶数),则9+n是该数列的( )
| A. | 第n+1项 | B. | 第n+2项 | C. | 第$\frac{n}{2}$+2项 | D. | 第$\frac{n}{2}$+3项 |
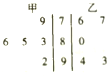 将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论:
将甲、乙两名学生近5次生物考试成绩,制成如图所示的茎叶图,考虑以下结论: