题目内容
（2012•江苏二模）选做题A．选修4-1：几何证明选讲
如图，自⊙O外一点P作⊙O的切线PC和割线PBA，点C为切点，割线PBA交⊙O于A，B两点，点O在AB上．作CD⊥AB，垂足为点D．
求证：
| PC |
| PA |
| BD |
| DC |
B．选修4-2：矩阵与变换
设a，b∈R，若矩阵A=
|
C．选修4-4：坐标系与参数方程
求椭圆C：
| x2 |
| 16 |
| y2 |
| 9 |
D．选修4-5不等式选讲
已知非负实数x，y，z满足x2+y2+z2+x+2y+3z=
| 13 |
| 4 |
分析：A．利用弦切角定理可以证明∠PCB=∠PAC，又∠BPC=∠CPA，从而有△PCB∽△PAC，得到比例式
=
，①又在直角三角形ABC中，有
=
，②，等量代换得
=
．
B．在直线l取两点M（2，0），N（0，-4），M，N在矩阵A对应的变换作业下分别对应于点M'，N'，分别求出点M'，N'的坐标，代入直线l′，建立方程组，解之即可．
C．先求出椭圆的参数方程点P（4cosθ，3sinθ）到直线l的距离d，再由和（差）角公式求出椭圆上的点到直线l的距离的最小值．
D．利用题中条件可化为：（x+
）2+（y+1）2+（x+
）2=
，根据柯西不等式可得到[（x+
）+（y+1）+（x+
）]2≤3[（x+
）2+（y+1）2+（x+
）]=
，从而求出x+y+z的最小值．
| PC |
| PA |
| BC |
| AC |
| BD |
| DC |
| BC |
| CA |
| PC |
| PA |
| BD |
| DC |
B．在直线l取两点M（2，0），N（0，-4），M，N在矩阵A对应的变换作业下分别对应于点M'，N'，分别求出点M'，N'的坐标，代入直线l′，建立方程组，解之即可．
C．先求出椭圆的参数方程点P（4cosθ，3sinθ）到直线l的距离d，再由和（差）角公式求出椭圆上的点到直线l的距离的最小值．
D．利用题中条件可化为：（x+
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 81 |
| 4 |
解答：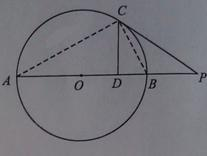
解：A．证明：连接BC、AC，
∵PC作⊙O的切线，切点为C，
∴∠PCB=∠PAC，
又∵∠BPC=∠CPA，
∴△PCB∽△PAC；
∴
=
，①
又在直角三角形ABC中，有
=
，②
由①②得
=
．
B：在直线l取两点M（2，0），N（0，-4）
M，N在矩阵A对应的变换作业下分别对应于点M'，N'
因
=
，所以M'的坐标为（2a，-2）；
=
，所以N'的坐标为（0，-4b）；
由题意可知M'，N'在直线l′上，
所以
解得：a=5，b=3．
C：∵设P（4cosθ，3sinθ）到直线l的距离：
d=
=
≥
当sin（θ+
）=-1时，等号成立，
故d的最小值为
．
D．条件可化为：（x+
）2+（y+1）2+（z+
）2=
则：[（x+
）+（y+1）+（z+
）]2≤3[（x+
）2+（y+1）2+（z+
）2]=
得x+y+z≤
，当且仅当：x+
=y+1=z+
时取等号，
∴x+y+z的最小值为：
．
解：A．证明：连接BC、AC，∵PC作⊙O的切线，切点为C，
∴∠PCB=∠PAC，
又∵∠BPC=∠CPA，
∴△PCB∽△PAC；
∴
| PC |
| PA |
| BC |
| AC |
又在直角三角形ABC中，有
| BD |
| DC |
| BC |
| CA |
由①②得
| PC |
| PA |
| BD |
| DC |
B：在直线l取两点M（2，0），N（0，-4）
M，N在矩阵A对应的变换作业下分别对应于点M'，N'
因
|
|
|
|
|
|
由题意可知M'，N'在直线l′上，
所以
|
解得：a=5，b=3．
C：∵设P（4cosθ，3sinθ）到直线l的距离：
d=
| |12cosθ+12sinθ+18| |
| 5 |
12
| ||||
| 5 |
-12
| ||
| 5 |
当sin（θ+
| π |
| 4 |
故d的最小值为
-12
| ||
| 5 |
D．条件可化为：（x+
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 4 |
则：[（x+
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 81 |
| 4 |
得x+y+z≤
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴x+y+z的最小值为：
| 3 |
| 2 |
点评：A．本题考查了弦切角定理，切线的性质定理，运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
B．本题主要考查了变换、矩阵的相等、几种特殊的矩阵变换，同时考查了计算能力，属于基础题．
C．本题以椭圆为载体，考查椭圆的参数方程、点到直线的距离公式、和（差）角公式，综合性强，考查函数与方程思想，化归与转化思想．
D．本题考查用柯西不等式求最值，关键是利用构造利用一般形式的柯西不等式．
B．本题主要考查了变换、矩阵的相等、几种特殊的矩阵变换，同时考查了计算能力，属于基础题．
C．本题以椭圆为载体，考查椭圆的参数方程、点到直线的距离公式、和（差）角公式，综合性强，考查函数与方程思想，化归与转化思想．
D．本题考查用柯西不等式求最值，关键是利用构造利用一般形式的柯西不等式．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
（2012•江苏二模）如图，已知A、B是函数y=3sin（2x+θ）的图象与x轴两相邻交点，C是图象上A，B之间的最低点，则
（2012•江苏二模）如图，在C城周边已有两条公路l1，l2在点O处交汇，现规划在公路l1，l2上分别选择A，B两处为交汇点（异于点O）直接修建一条公路通过C城，已知OC=