题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,求证:
时,求证:![]() ;
;
(3)设函数![]() ,其中
,其中![]() 为实常数,试讨论函数
为实常数,试讨论函数![]() 的零点个数,并证明你的结论.
的零点个数,并证明你的结论.
【答案】(1)![]() (2)见证明;(3)见解析
(2)见证明;(3)见解析
【解析】
(1)根据题意求出函数![]() 的导函数,表示出切点的纵坐标,根据导数的几何意义列出方程,由此即可求出切点的横坐标;
的导函数,表示出切点的纵坐标,根据导数的几何意义列出方程,由此即可求出切点的横坐标;
(2)设![]() ,求出函数的导函数
,求出函数的导函数![]() ,令
,令![]() ,列出表格,观察即可判断出函数的最小值,从而证明
,列出表格,观察即可判断出函数的最小值,从而证明![]() ;
;
(3)根据题意![]() ,构造出函数
,构造出函数![]() ,求出函数的导函数
,求出函数的导函数![]() ,分情况讨论b的取值范围,当b≤0,根据
,分情况讨论b的取值范围,当b≤0,根据![]() 与0的关系判断出
与0的关系判断出![]() 的零点个数;其次当b>0时,结合x的范围判断出函数的单调性,这里要注意当x>2时,根据b的范围即
的零点个数;其次当b>0时,结合x的范围判断出函数的单调性,这里要注意当x>2时,根据b的范围即![]() 、
、![]() 和
和![]() 来判断
来判断![]() 的零点,由此即可知
的零点,由此即可知![]() 的零点个数.
的零点个数.
(1)![]() . 因为切线
. 因为切线![]() 过原点
过原点![]() ,
,
所以 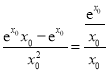 ,解得:
,解得:![]() .
.
(2)设![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() .
.
![]() 在
在![]() 上变化时,
上变化时,![]() 的变化情况如下表
的变化情况如下表
x | (0,2) | 2 |
|
| - | 0 | + |
|
|
|
|
所以 当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
所以 当![]() 时,
时,![]() ,即
,即![]() .
.
(3)![]() 等价于
等价于![]() ,等价于
,等价于![]() .注意
.注意![]() .
.
令![]() ,所以
,所以![]() .
.
(I)当![]() 时,
时, ![]() ,所以
,所以![]() 无零点,即
无零点,即![]() 在定义域内无零点.
在定义域内无零点.
(II)当![]() 时,(i)当
时,(i)当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
因为![]() 在
在![]() 上单调递增,而
上单调递增,而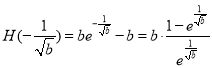 ,
,
又![]() ,所以
,所以![]() .
.
又因为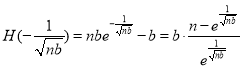 ,其中
,其中![]() ,
,
取![]() ,
,![]() 表示
表示![]() 的整数部分.所以
的整数部分.所以![]() ,
,![]() ,由此
,由此![]() .
.
由零点存在定理知,![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
(ii)当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以当![]() 时,
时,![]() 有极小值也是最小值,
有极小值也是最小值,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上不存在零点;
上不存在零点;
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上存在唯一零点2;
上存在唯一零点2;
③当![]() ,即
,即![]() 时,由
时,由![]() 有
有![]() ,
,
而![]() ,所以
,所以![]() 在
在![]() 上存在唯一零点;
上存在唯一零点;
又因为![]() ,
,![]() .
.
令![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,因此
,因此![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() ,
,
所以![]() 在
在![]() 上单调递增,因此
上单调递增,因此![]() ,
,
故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() .
.
由上得![]() ,由零点存在定理知,
,由零点存在定理知,![]() 在
在![]() 上存在唯一零点,即在
上存在唯一零点,即在![]() 上存在唯一零点.
上存在唯一零点.
综上所述:当![]() 时,函数
时,函数![]() 的零点个数为0;
的零点个数为0;
当![]() 时,函数
时,函数![]() 的零点个数为1;
的零点个数为1;
当![]() 时,函数
时,函数![]() 的零点个数为2;
的零点个数为2;
当![]() 时,函数
时,函数![]() 的零点个数为3.
的零点个数为3.