题目内容
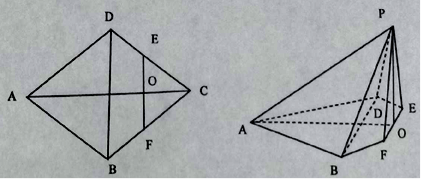
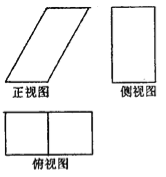
【题目】一个几何体的三视图如图所示，已知正（主）视图是底边长为1的平行四边形，侧（左）视图是一个长为
，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．
（1）求该几何体的体积
；
（2）求该几何体的表面积
．
【答案】（1）
；（2）
．
【解析】
试题分析：（1）根据正视图是底面边长为
的平行四边形，侧视图是个长为
，宽为
的矩形，得到该几何体是一个平行六面体，其底面是边长为
的正方形，高为，即可求解体积；（2）由（1）看出的几何体，知道该平行六面体中，
面
，
面
，得到侧棱长，表示几何体的表面积，得到结果．
试题解析：（1）由三视图可知，该几何体是一个平行六面体（如图），其底面是边长为1的正方形，高为
，所以
．
（2）由三视图可知，
该平行六面体中
平面
，
平面
，
∴
，侧面
，
均为矩形，
．
练习册系列答案
相关题目
【题目】为了参加市高中篮球比赛，某中学决定从四个篮球较强的班级的篮球队员中选出
人组成男子篮球队，代表该地区参赛，四个篮球较强的班级篮球队员人数如下表：
班级 | 高三（7）班 | 高三（17）班 | 高二（31）班 | 高二（32）班 |
人数 | 12 | 6 | 9 | 9 |
（1）现采取分层抽样的方法从这四个班中抽取运动员，求应分别从这四个班抽出的队员人数；
（2）该中学篮球队奋力拼搏，获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言，求选出的两名队员来自同一班的概率.
