题目内容
在直三棱柱ABC-A1B1C1中，底面为直角三角形∠ACB=90°，AC=| 2 |
分析：连A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，不难看出CP+PA1的最小值是A1C的连线．（在BC1上取一点与A1C构成三角形，因为三角形两边和大于第三边）由余弦定理即可求解．
解答：
解：连A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，如图所示，
连A1C，则A1C的长度就是所求的最小值．
通过计算可得∠A1C1P=90°又∠BC1C=45°
∴∠A1C1C=135°
由余弦定理可求得A1C=
故选B．
解：连A1B，沿BC1将△CBC1展开与△A1BC1在同一个平面内，如图所示，连A1C，则A1C的长度就是所求的最小值．
通过计算可得∠A1C1P=90°又∠BC1C=45°
∴∠A1C1C=135°
由余弦定理可求得A1C=
| 5 |
故选B．
点评：本题考查棱柱的结构特征，余弦定理的应用，是中档题．
练习册系列答案
53天天练系列答案
相关题目
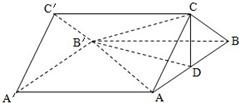如图，在直三棱柱ABC-A′B′C′中，已知AA′=4，AC=BC=2，∠ACB=90°，D是AB的中点．
（2012•泸州一模）如图，在直三棱柱ABC-A′B′C′中，AB=BC=CA=a，
如图，在直三棱柱ABC-A′B′C′中，AA′=AB=BC=1，∠ABC=90°．棱A′C′上有两个动点E，F，且EF=a （a为常数）．
如图所示，在直三棱柱ABC-A′B′C′中，∠BAC=90°，AB=BB′=1，直线B′C与平面ABC成30°角．
如图，在直三棱柱ABC-A′B′C′中，点D是BC的中点，∠ACB=90°，AC=BC=1，AA′=2，