题目内容
20.已知P(2,-3)是角θ终边上一点,则tan(2π+θ)等于( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
分析 由条件利用任意角的三角函数的定义、诱导公式求得tan(2π+θ)的值.
解答 解:∵P(2,-3)是角θ终边上一点,∴tanθ=$\frac{-3}{2}$=-$\frac{3}{2}$,
则tan(2π+θ)=tanθ=-$\frac{3}{2}$,
故选:C.
点评 本题主要考查任意角的三角函数的定义、诱导公式,属于基础题.

练习册系列答案
相关题目
15.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且当x∈[-1,0)时f(x)=($\frac{1}{2}$)x,则 f(log28)等于( )
| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
5.已知全集U={x∈Z|x2-3x-10<0},集合P={0,3},Q=|2,0,1},则∁U(P∪Q)=( )
| A. | {-1,4,5} | B. | {-1,4} | C. | {-1,1,2,3,4} | D. | {1,2,3} |
12.实数x,y,z满足x2+y2+z2=1,则xy-yz的最小值为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{4}$ |
 中,
中,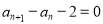 ,且
,且 ,则
,则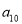 等于( )
等于( )