题目内容
1．如图是一个三棱锥的三视图，俯视图是一个斜边长为2的直角三角形，设它的外接球的表面积为S，则（ ）
| A． | S是定值，S=8π | B． | S不是定值，有最小值Smin=8π | ||
| C． | S不是定值，有最大值Smax=8π | D． | S不是定值，与a的大小有关 |
分析 由已知中的三视力可得该几何体是一个三棱锥，计算出外接球的表面积S，可得答案．
解答 解：∵三棱锥的三视图中俯视图是一个斜边长为2的直角三角形，
故棱锥底面的外接圆半径r=1，
由棱锥的高为2，
故棱锥外接球球心到底面的距离d=1，
故圆锥的外接球半径R=$\sqrt{2}$，
故圆锥的外接球表面积S=8π，
故选：A
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
4．若log2a，log2b是方程x2+x-3=0的两根，则（lg$\frac{a}{b}$）2等于（ ）
| A． | 13 | B． | 13（lg2）2 | C． | 10 | D． | 10（lg2） |
16．
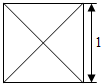已知某几何体的俯视图是如图所示的边长为1的正方形，主视图与左视图是边长为1的正三角形，则其全面积是（ ）
已知某几何体的俯视图是如图所示的边长为1的正方形，主视图与左视图是边长为1的正三角形，则其全面积是（ ）| A． | 2 | B． | 3 | C． | $1+\sqrt{3}$ | D． | $\sqrt{3}$ |
6．直三棱柱ABC-A1B1C1中，∠A1B1C1=90°，且AB=BC=BB1，E，F分别是AB，CC1的中点，那么直线A1C与EF所成的角的余弦值为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{\sqrt{2}}{3}$ |
13．如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（ ）
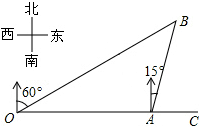
| A． | 4km | B． | 2$\sqrt{3}$km | C． | 2$\sqrt{2}$km | D． | （$\sqrt{3}$+1）km |