题目内容
(本题12分)
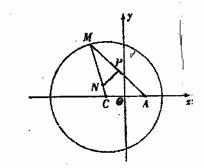
如图所示,已知圆![]() 定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足![]() ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
(I)求曲线E的方程;
(II)
|
| |
(本小题满分12分)
解:答案:(1)![]()
∴NP为AM的垂直平分线, ∴|NA|=|NM|
又![]()
![]()
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆…………┅……2分
且椭圆长轴长为![]() …………………………………………4分
…………………………………………4分
![]() ∴曲线E的方程为
∴曲线E的方程为![]() ………………………6分
………………………6分
(2)当直线GH斜率存在时,
设直线GH方程为![]()
得![]() 由
由![]()
设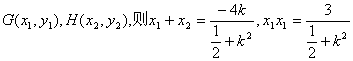 ……………8分
……………8分
又![]()
![]()
![]()
![]()
![]()
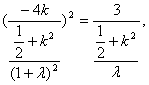
整理得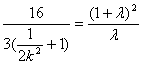 ……………………………………………………10分
……………………………………………………10分
![]()
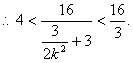
![]() 又
又![]()
![]()
又当直线GH斜率不存在,方程为![]()
![]() 即所求
即所求![]() 的取值范围是
的取值范围是![]() ………………………………………12分
………………………………………12分

练习册系列答案
相关题目
 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
 中,
中,  ,点
,点 是棱
是棱 上一点.
上一点.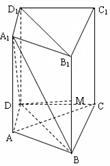
 面
面 ;
; ;
; 中,
中,  ,点
,点 是棱
是棱 上一点
上一点 面
面 ;
; ;
;
 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.