题目内容
设等差数列{an}的前n项和Sn,且a1+a2+a3=4,a7+a8+a9=16,则S9=
- A.28
- B.30
- C.42
- D.48
B
分析:根据等差数列的通项公式化简已知的两等式得到两个关系式,然后把两关系式相减即可求出等差d,把公差d的值代入到两关系式中任意一个即可求出首项,然后根据等差和首项即可求出S9的值.
解答:由已知可知:a1+a2+a3=3a1+3d=4①,a7+a8+a9=3a1+21d=16②,
②-①得:18d=12,解得:d= ,把d=
,把d= 代入①得:a1=
代入①得:a1= ,
,
则S9=9× +
+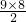 ×
× =30.
=30.
故选B
点评:此题考查学生掌握等差数列的性质,灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道综合题.
分析:根据等差数列的通项公式化简已知的两等式得到两个关系式,然后把两关系式相减即可求出等差d,把公差d的值代入到两关系式中任意一个即可求出首项,然后根据等差和首项即可求出S9的值.
解答:由已知可知:a1+a2+a3=3a1+3d=4①,a7+a8+a9=3a1+21d=16②,
②-①得:18d=12,解得:d=
 ,把d=
,把d= 代入①得:a1=
代入①得:a1= ,
,则S9=9×
 +
+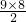 ×
× =30.
=30.故选B
点评:此题考查学生掌握等差数列的性质,灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道综合题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目