题目内容
【题目】已知函数f(x)= ![]() 函数g(x)=2﹣f(x),若函数y=f(x)﹣g(x)恰有4个零点,则实数a的取值范围是 .
函数g(x)=2﹣f(x),若函数y=f(x)﹣g(x)恰有4个零点,则实数a的取值范围是 .
【答案】(2,3]
【解析】解:由题意当y=f(x)﹣g(x)=2[f(x)﹣1]=0 时,即方程f(x)=1 有4个解.
又由函数y=a﹣|x+1|与函数y=(x﹣a)2 的大致形状可知,
直线y=1 与函数f(x)= ![]() 的左右两支曲线都有两个交点,
的左右两支曲线都有两个交点,
当x≤1时,函数f(x)的最大值为a,则a>1,
同时在[﹣1,1]上f(x)=a﹣|x+1|的最小值为f(1)=a﹣2,
当a>1时,在(1,a]上f(1)=(1﹣a)2 ,
要使y=f(x)﹣g(x)恰有4个零点,
则满足 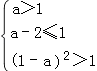 ,即
,即 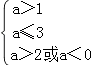 ,解得2<a≤3.
,解得2<a≤3.
所以答案是:(2,3]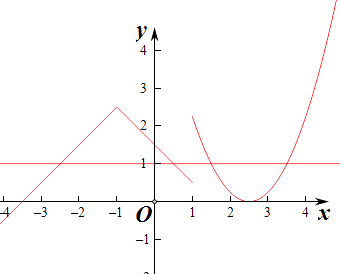

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目