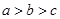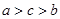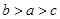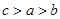题目内容
函数f(x)=-(cosx)|lg|x||的部分图象是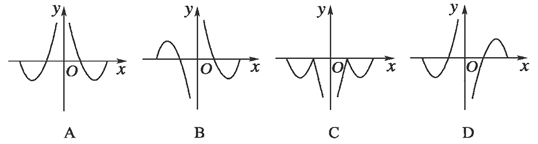

C
因为f(x)=-(cosx)|lg|x||
∴f(-x)=-(cos(-x))|lg|-x||=f(x),故是偶函数,
由此可确定是A或C选项中的一个,
下用特殊值法判断,通过分离函数得
f1(x)=-cosx,f2(x)=|lg|x||,
由于f2(x)=|lg|x||≥0,
观察函数f1(x)=-cosx的符号即可,
由于x∈(-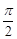 ,0)∪(0,
,0)∪(0,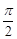 )时,
)时,
f1(x)=-cosx<0,
表明函数图象在x∈(-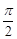 ,0)∪(0,
,0)∪(0,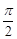 )时位于x轴下方,
)时位于x轴下方,
故选C.
∴f(-x)=-(cos(-x))|lg|-x||=f(x),故是偶函数,
由此可确定是A或C选项中的一个,
下用特殊值法判断,通过分离函数得
f1(x)=-cosx,f2(x)=|lg|x||,
由于f2(x)=|lg|x||≥0,
观察函数f1(x)=-cosx的符号即可,
由于x∈(-
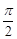 ,0)∪(0,
,0)∪(0,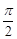 )时,
)时,f1(x)=-cosx<0,
表明函数图象在x∈(-
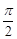 ,0)∪(0,
,0)∪(0,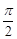 )时位于x轴下方,
)时位于x轴下方,故选C.

练习册系列答案
相关题目
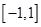 上的偶函数
上的偶函数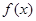 ,已知当
,已知当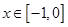 时的解析式
时的解析式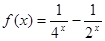
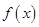 在
在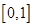 上的解析式;
上的解析式;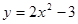
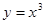
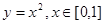
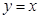
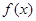 为奇函数,
为奇函数,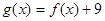 ,
,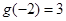 ,求
,求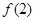
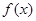 的定义域为D,如果对于任意的
的定义域为D,如果对于任意的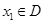 ,存在唯一的
,存在唯一的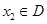 ,使得
,使得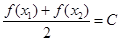 成立(其中C为常数),则称函数
成立(其中C为常数),则称函数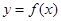 在D上的约算术均值为C,则下列函数在其定义域上的算术均值可以为2的函数是 ( )
在D上的约算术均值为C,则下列函数在其定义域上的算术均值可以为2的函数是 ( )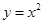
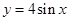
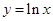

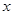 ,都有
,都有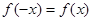 ,且
,且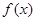 在(-∞,0]上是增函数,则( )
在(-∞,0]上是增函数,则( ) 


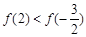
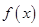 在
在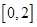 上递减,试比
上递减,试比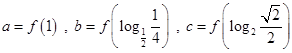 大小
大小