题目内容
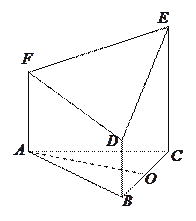
【题目】如图![]() ,在梯形
,在梯形![]() 中,
中, ![]() 于
于![]() ,
, ![]()
![]() .将
.将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2),
(如图2), ![]() 为线段
为线段![]() 上一点.
上一点.

图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为线段
为线段![]() 中点,求多面体
中点,求多面体![]() 与多面体
与多面体![]() 的体积之比;
的体积之比;
(Ⅲ)是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长.若不存在,请说明理由.
的长.若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)折起后仍有![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
, ![]() ;(Ⅱ)直接求出三棱锥
;(Ⅱ)直接求出三棱锥![]() 的体积,利用分割法求出
的体积,利用分割法求出![]() ,从而可得结果;(Ⅲ)根据三角形相似可得
,从而可得结果;(Ⅲ)根据三角形相似可得![]() ,由线面平行的性质定理可得
,由线面平行的性质定理可得![]() ,由中位线定理可得
,由中位线定理可得![]() ,
,![]() ,
,![]() 在
在![]() 中,
中, ![]() ,
,![]() .
.
试题解析:(Ⅰ)在梯形![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
, ![]() .
.
(Ⅱ)![]() 为
为![]() 中点,
中点,
![]() 到底面
到底面![]() 的距离为
的距离为![]() ,
,
在梯形![]() 中,
中, ![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() 在
在![]() 中,
中, ![]() ,
,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
, ![]() ,
,
![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
![]() ,
,![]() .
.
![]() .
.
(Ⅲ)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
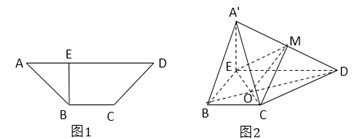
在四边形![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中, ![]() ,
,![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目