题目内容
12.已知f(x)=ax2+2x在[2,4]上单调,则a的取值范围是a≤-$\frac{1}{2}$或a≥-$\frac{1}{4}$.分析 当a=0时,f(x)为一次函数,符合题意,当a≠0时,f(x)为二次函数,则[2,4]在对称轴某一侧.
解答 解:当a=0时,f(x)=2x,在[2,4]上是增函数,符合题意;
当a≠0时,f(x)为二次函数,对称轴为x=-$\frac{1}{a}$,
∵f(x)=ax2+2x在[2,4]上单调,
∴-$\frac{1}{a}$≤2或-$\frac{1}{a}$≥4,
解得a>0,或a≤-$\frac{1}{2}$,或-$\frac{1}{4}$≤a<0.
综上,a的取值范围是a≤-$\frac{1}{2}$或a≥-$\frac{1}{4}$.
故答案为a≤-$\frac{1}{2}$或a≥-$\frac{1}{4}$.
点评 本题考查了二次函数的单调性与对称轴的关系,分类讨论思想,对a进行讨论是本题的关键,属于基础题.

练习册系列答案
相关题目
1.已知函数f(x)=ax+7,f(-3)=5,则f(3)的值为( )
| A. | 9 | B. | -9 | C. | -5 | D. | 7 |
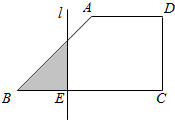 如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.
如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.