题目内容
【题目】已知函数f（x）=4cosωxsin（ωx+ 
）（ω＞0）的最小正周期为π．
（1）求ω的值；
（2）讨论f（x）在区间[0， 
]上的单调性；
（3）当x∈[0， ]时，关于x的方程f（x）=a 恰有两个不同的解，求实数a的取值范围．
【答案】
（1）解：f（x）=4cosωxsin（ωx+ 
）
=2 
sinωxcosωx+2 cos2ωx，
= （sin 2ωx+cos 2ωx）+ ，
=2sin（2ωx+ ）+ ，
因为f（x）的最小正周期为π，且ω＞0，从而有 
=π，
故ω=1
（2）解：由（1）知，f（x）=2sin（2x+ ）+ ．若0≤x≤ 
，则 ≤2x+ ≤ 
．
当 ≤2x+ ≤ ，即0≤x≤ 
时，f（x）单调递增；
当 ≤2x+ ≤ ，即 ≤x≤ 时，f（x）单调递减．
综上可知，f（x）在区间[0， ]上单调递增，在区间[ ， ]上单调递减
（3）解：x∈[0， ]时，关于x的方程f（x）=a 恰有两个不同的解，
即y=a与函数在[0， ]上，与f（x）=2sin（2x+ ）+ 由两个交点，
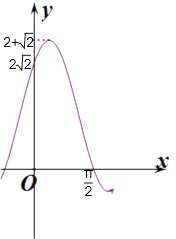
由函数图象可知：a∈[2 ，2+ ），
实数a的取值范围[2 ，2+ ）
【解析】（1）由两角和的正弦公式及辅助角公式化简f（x），根据周期公式即可求得ω的值；（2）由（1）求得f（x）的解析式，根据正弦函数图象及性质即可判断函数区间[0， ]上的单调性；（3）由题意可知y=a与函数在[0， ]上，与f（x）=2sin（2x+ ）+ 由两个交点，根据函数图象即可求得实数a的取值范围．
练习册系列答案
阅读快车系列答案
相关题目
