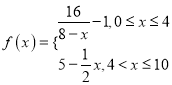题目内容
【题目】若![]() 、
、![]() 两点分别在函数
两点分别在函数![]() 与
与![]() 的图像上,且关于直线
的图像上,且关于直线![]() 对称,则称
对称,则称![]() 、
、![]() 是
是![]() 与
与![]() 的一对“伴点”(
的一对“伴点”(![]() 、
、![]() 与
与![]() 、
、![]() 视为相同的一对).已知
视为相同的一对).已知 ,
,![]() ,若
,若![]() 与
与![]() 存在两对“伴点”,则实数
存在两对“伴点”,则实数![]() 的取值范围为________.
的取值范围为________.
【答案】![]()
【解析】
求出![]() 关于直线
关于直线![]() 的对称图象所对应的函数解析式
的对称图象所对应的函数解析式![]() ,画出图形,再由函数图象的平移结合新定义求解实数
,画出图形,再由函数图象的平移结合新定义求解实数![]() 的取值范围.
的取值范围.
解:设曲线![]() 关于
关于![]() 的对称图象上的点为
的对称图象上的点为![]() ,
,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
则![]() ,
,![]() ,代入
,代入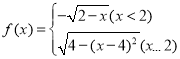 ,得
,得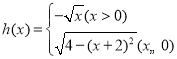 .
.
作出函数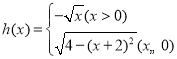 的图象如图,
的图象如图,
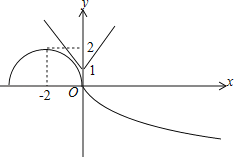
函数![]() 的图象是把
的图象是把![]() 向左
向左![]() 或向右
或向右![]() 平移
平移![]() 个单位得到的.
个单位得到的.
由图可知,要使![]() 与
与![]() 存在两对“伴点”,需要把
存在两对“伴点”,需要把![]() 向左平移.
向左平移.
则![]() ,设直线
,设直线![]() ,即
,即![]() ,
,
由圆心![]() 到直线的距离为2,得
到直线的距离为2,得![]() ,解得
,解得![]() 或
或![]() (舍
(舍![]() ;
;
设直线![]() ,即
,即![]() ,
,
由圆心![]() 到直线的距离为2,得
到直线的距离为2,得![]() ,解得
,解得![]() 或
或![]() (舍
(舍![]() .
.
![]() 要使
要使![]() 与
与![]() 存在两对“伴点”,则实数
存在两对“伴点”,则实数![]() 的取值范围为
的取值范围为![]()
故答案为:![]()

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: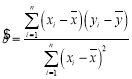 ,
,![]() .
.