Question

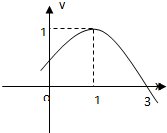f（x）=cos（wx+?）（w＞0，0≤?≤2π）部分图象如图则

8

x=1

f（x）=（　　）

• A．0
• B．-

  2

  2

• C．

  2

  2

• D．1

Answer 1

分析：依题意可知，

1

4

T=2，从而可求得w，再由w×1+φ=2kπ（k∈Z），0≤?≤2π可求得φ，从而可得f（x）的解析式，继而可求得则

8

x=1

f（x）．

解答：解：由图知，

1

4

T=2，又w＞0，
∴T=

2π

w

=8，
∴w=

π

4

；
又f（x）=cos（wx+?）经过（1，1），
∴w×1+φ=2kπ（k∈Z），即
∴φ=2kπ-w=2kπ-

π

4

（k∈Z），
又0≤?≤2π，
∴φ=

7π

4

，
∴f（x）=cos（

π

4

x+

7π

4

）=cos（

π

4

x-

π

4

），
∴

8

x=1

f（x）=f（1）+f（2）+…+f（8）=1+

2

2

+0-

2

2

-1-

2

2

+0+

2

2

=0．
故选A．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求得f（x）=cos（

π

4

x+

7π

4

）是关键，考查推理与运算能力，属于中档题．