题目内容
已知下列命题:
①函数y=sin(-2x+
)的单调增区间是[-kπ-
,-kπ+
](k∈Z).
②要得到函数y=cos(x-
)的图象,需把函数y=sinx的图象上所有点向左平行移动
个单位长度.
③已知函数f(x)=2cos2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则w≥
π.
其中正确命题的序号是______.
①函数y=sin(-2x+
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
②要得到函数y=cos(x-
| π |
| 6 |
| π |
| 3 |
③已知函数f(x)=2cos2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则w≥
| 399 |
| 2 |
其中正确命题的序号是______.
y=sin(-2x+
)=sin[π-(-2x+
)]=y=sin(2x+
),
由2x+
∈[2kπ-
,2kπ+
](k∈Z)得:x∈[kπ-
,kπ-
](k∈Z)
即函数y=sin(-2x+
)的单调增区间是[kπ-
,kπ-
](k∈Z),故①错误;
把函数y=sinx的图象上所有点向左平行移动
个单位长度,可得函数y=y=sin(x+
)=sin[(x-
)+
]=cos(x-
)的图象,故②正确;
令t=cosx,t∈[-1,1],则函数f(x)=2cos2x-2acosx+3可化为y=2t2-2at+3,若a≤-2时,则t=-1时,函数f(x)的最小值为5+2a,故③正确.
∵y=sinwx在y轴右侧第一次取最小值时,在
个周期处,故y=sinwx(w>0)在[0,1]上至少出现了100次最小值,说明在[0,1]上至少有99
个周期,
则1≥99
×T,即1≥99
×
,解得w≥
π,故④正确.
故答案为:②③④
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
由2x+
| 2π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 7π |
| 12 |
| π |
| 12 |
即函数y=sin(-2x+
| π |
| 3 |
| 7π |
| 12 |
| π |
| 12 |
把函数y=sinx的图象上所有点向左平行移动
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
令t=cosx,t∈[-1,1],则函数f(x)=2cos2x-2acosx+3可化为y=2t2-2at+3,若a≤-2时,则t=-1时,函数f(x)的最小值为5+2a,故③正确.
∵y=sinwx在y轴右侧第一次取最小值时,在
| 3 |
| 4 |
| 3 |
| 4 |
则1≥99
| 3 |
| 4 |
| 3 |
| 4 |
| 2π |
| ω |
| 399 |
| 2 |
故答案为:②③④

练习册系列答案
相关题目
 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动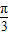 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数
的图象,需把函数 的图象上所有点向左平行移动
的图象上所有点向左平行移动 个单位长度.
个单位长度. ,当
,当 时,函数
时,函数 的最小值为
的最小值为 .
. 在[0,1]上至少出现了100次最小值,则
在[0,1]上至少出现了100次最小值,则 .
. ②函数
②函数 的图象向左平移1个单位后得到的函数图象解析式为
的图象向左平移1个单位后得到的函数图象解析式为 ;③函数
;③函数 满足
满足 ,则函数
,则函数 对称;④满足条件
对称;④满足条件 的三角形
的三角形 有两个,其中正确命题的序号是 。
有两个,其中正确命题的序号是 。