题目内容
已知下列命题:
①函数y=sin(-2x+
)的单调增区间是[-kπ-
,-kπ+
](k∈Z).
②要得到函数y=cos(x-
)的图象,需把函数y=sinx的图象上所有点向左平行移动
个单位长度.
③已知函数f(x)=2cos2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则w≥
π.
其中正确命题的序号是
①函数y=sin(-2x+
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
②要得到函数y=cos(x-
| π |
| 6 |
| π |
| 3 |
③已知函数f(x)=2cos2x-2acosx+3,当a≤-2时,函数f(x)的最小值为g(a)=5+2a.
④y=sinwx(w>0)在[0,1]上至少出现了100次最小值,则w≥
| 399 |
| 2 |
其中正确命题的序号是
②③④
②③④
.分析:根据正弦函数的单调性,求出函数y=sin(-2x+
)的单调增区间,进而判断①的真假;
根据正弦型函数图象的平移变换法则,求出平移后的函数解析式,与已知函数解析式进行比较可判断②的真假;
根据余弦函数的值域及二次函数的图象和性质分析出函数的最小值,即可判断③的真假;
根据正弦型函数的图象和周期性,分析出满足条件时,周期的范围,进而求出ω的范围,可判断④的真假;
| π |
| 3 |
根据正弦型函数图象的平移变换法则,求出平移后的函数解析式,与已知函数解析式进行比较可判断②的真假;
根据余弦函数的值域及二次函数的图象和性质分析出函数的最小值,即可判断③的真假;
根据正弦型函数的图象和周期性,分析出满足条件时,周期的范围,进而求出ω的范围,可判断④的真假;
解答:解:y=sin(-2x+
)=sin[π-(-2x+
)]=y=sin(2x+
),
由2x+
∈[2kπ-
,2kπ+
](k∈Z)得:x∈[kπ-
,kπ-
](k∈Z)
即函数y=sin(-2x+
)的单调增区间是[kπ-
,kπ-
](k∈Z),故①错误;
把函数y=sinx的图象上所有点向左平行移动
个单位长度,可得函数y=y=sin(x+
)=sin[(x-
)+
]=cos(x-
)的图象,故②正确;
令t=cosx,t∈[-1,1],则函数f(x)=2cos2x-2acosx+3可化为y=2t2-2at+3,若a≤-2时,则t=-1时,函数f(x)的最小值为5+2a,故③正确.
∵y=sinwx在y轴右侧第一次取最小值时,在
个周期处,故y=sinwx(w>0)在[0,1]上至少出现了100次最小值,说明在[0,1]上至少有99
个周期,
则1≥99
×T,即1≥99
×
,解得w≥
π,故④正确.
故答案为:②③④
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
由2x+
| 2π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 7π |
| 12 |
| π |
| 12 |
即函数y=sin(-2x+
| π |
| 3 |
| 7π |
| 12 |
| π |
| 12 |
把函数y=sinx的图象上所有点向左平行移动
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
令t=cosx,t∈[-1,1],则函数f(x)=2cos2x-2acosx+3可化为y=2t2-2at+3,若a≤-2时,则t=-1时,函数f(x)的最小值为5+2a,故③正确.
∵y=sinwx在y轴右侧第一次取最小值时,在
| 3 |
| 4 |
| 3 |
| 4 |
则1≥99
| 3 |
| 4 |
| 3 |
| 4 |
| 2π |
| ω |
| 399 |
| 2 |
故答案为:②③④
点评:本题以命题的真假判断为载体考查了三角函数的图象和性质及平移变换,熟练掌握三角函数的图象和性质是解答的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数y=sinx的图象上所有点向左平行移动
的图象,需把函数y=sinx的图象上所有点向左平行移动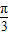 个单位长度.
个单位长度. .
. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数
的图象,需把函数 的图象上所有点向左平行移动
的图象上所有点向左平行移动 个单位长度.
个单位长度. ,当
,当 时,函数
时,函数 的最小值为
的最小值为 .
. 在[0,1]上至少出现了100次最小值,则
在[0,1]上至少出现了100次最小值,则 .
. ②函数
②函数 的图象向左平移1个单位后得到的函数图象解析式为
的图象向左平移1个单位后得到的函数图象解析式为 ;③函数
;③函数 满足
满足 ,则函数
,则函数 对称;④满足条件
对称;④满足条件 的三角形
的三角形 有两个,其中正确命题的序号是 。
有两个,其中正确命题的序号是 。